Convertir Fracciones a Decimales
De fracción a decimal – DIVIDIR
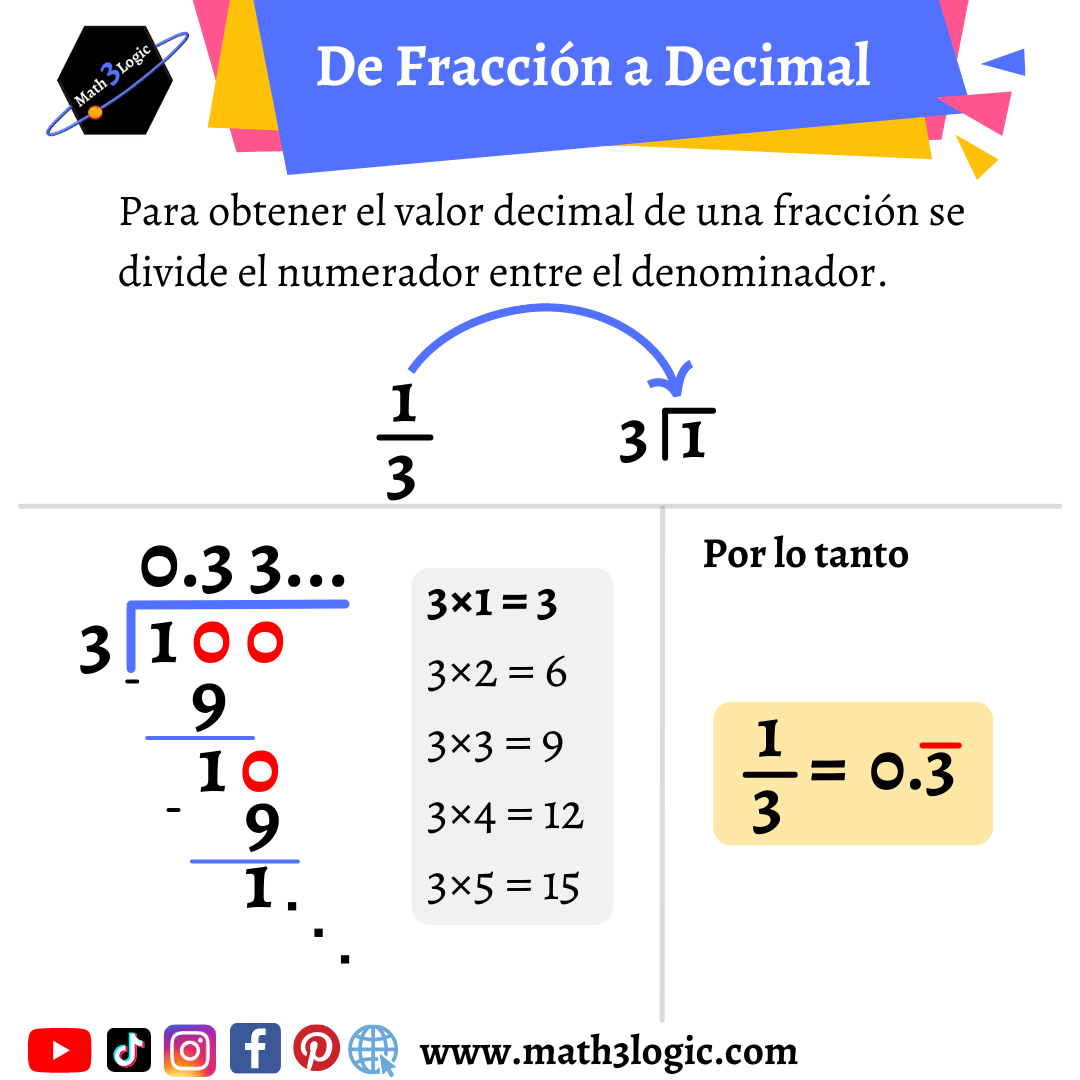
Para convertir una fracción a su escritura decimal se divide el numerador entre el denominador.
Barra periódica ̅
También conocida como vinculum o barra de repetición ̅Se utiliza para indicar que los dígitos debajo de la barra se repiten infinitamente en un patrón periódico en el número decimal. Por ejemplo, en el número decimal periódico 0.333…, la barra se coloca sobre el 3 para indicar que ese dígito se repite infinitamente.
DIFERENTES CASOS
Se sabe que para convertir una fracción a decimal se divide el numerador entre el denominador. Sin embargo, durante este proceso de conversión pueden surgir ciertos escenarios que es importante tener en cuenta, que pueden (en ciertos casos) facilitar que la conversión sea más sencilla y eficiente.
1.- Fracciones decimales: Son fracciones con denominador de potencias de 10 (10, 100, 100, etc.)
Estas fracciones son las más sencilla de convertir ya que su transformación decimal es directa, sin necesidad de realizar una división. Este tema lo puedes ver con mayor profundidad en la siguiente sección.
Se coloca el numerador y se mueve el punto decimal hacia la izquierda de acuerdo con la cantidad de ceros en el denominador, observa la imagen.
2.- Fracciones con valor decimal finito
En este caso, al dividir el numerador entre el denominador, el valor decimal resultante es un número con dígitos finitos después del punto decimal.
Ejemplo
4/5 = 0.8
3/8 = 0.375
1/4 = 0.25
¡Importante!
Ciertas fracciones cuyo valor decimal es finito son ampliamente utilizadas, como 1/2, 1/4 y 1/5. Estas fracciones y sus múltiplos se emplean para simplificar y acelerar el proceso de obtener valores decimales, evitando la necesidad de realizar divisiones complejas.
| Fracción | Decimal |
|---|---|
| 1/2 | 0.50 |
| 2/2 | 1 |
| 3/2 | 1.50 |
| 4/2 | 2 |
| Fracción | Decimal |
|---|---|
| 1/4 | 0.25 |
| 2/4 | 0.50 |
| 3/4 | 0.75 |
| 4/4 | 1 |
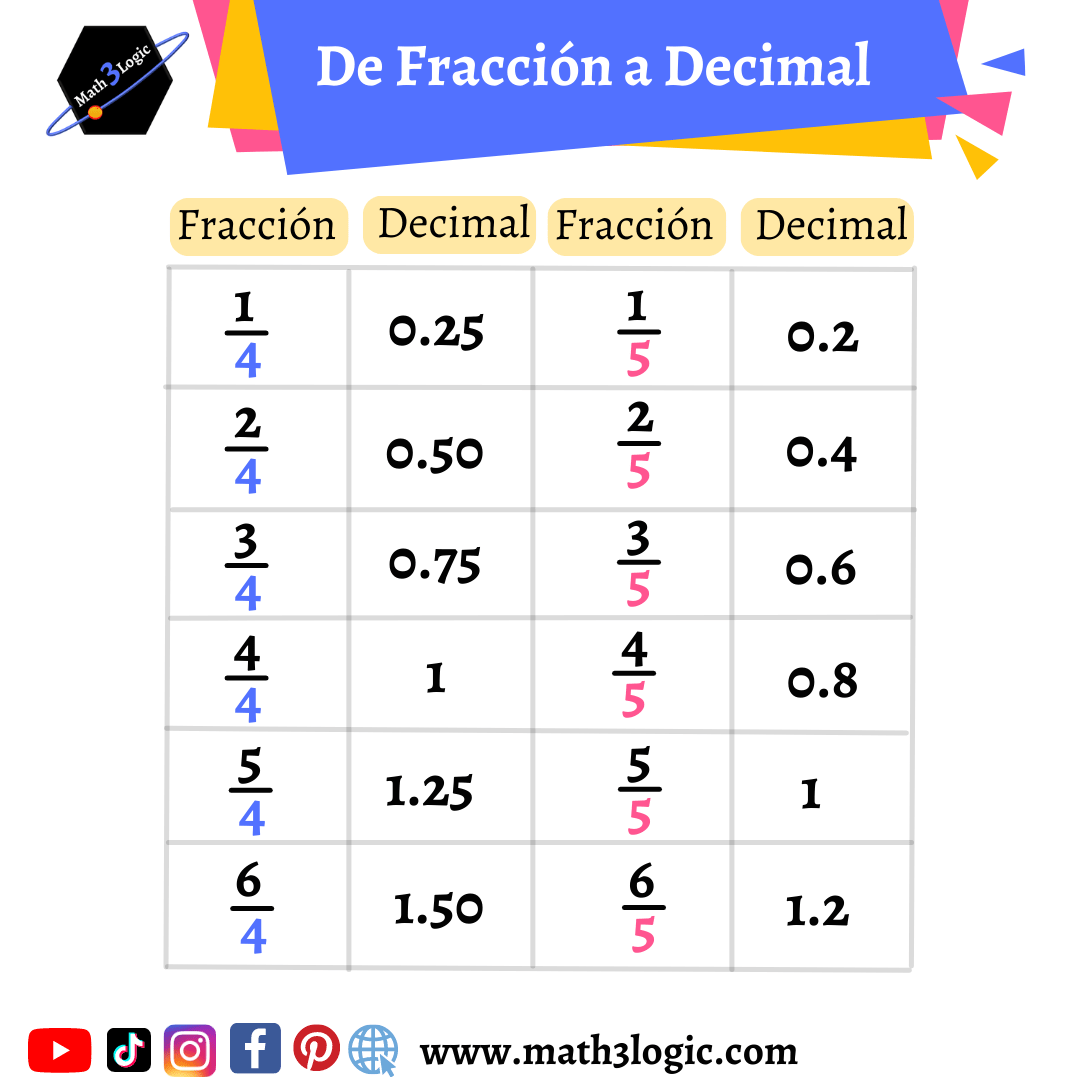
| Fracción | Decimal |
|---|---|
| 1/5 | 0.2 |
| 2/5 | 0.4 |
| 3/5 | 0.6 |
| 4/5 | 0.8 |
| 5/5 | 1 |
3.- Fracciones con valores decimales periódicos simples
Son aquellas en las que un solo dígito o un grupo de dígitos se repiten infinitamente en la parte decimal. Al dividir el numerador entre el denominador se observa el patrón de repetición. Se usa la barra periódica ⁻ arriba del número o del grupo de números que se repiten.
Ejemplo
1/3 = 0. 3333… = 0.3̅
1/9 = 0.11111… = 0.1̅
2/11 = 0.181818… = 0.1̅8̅
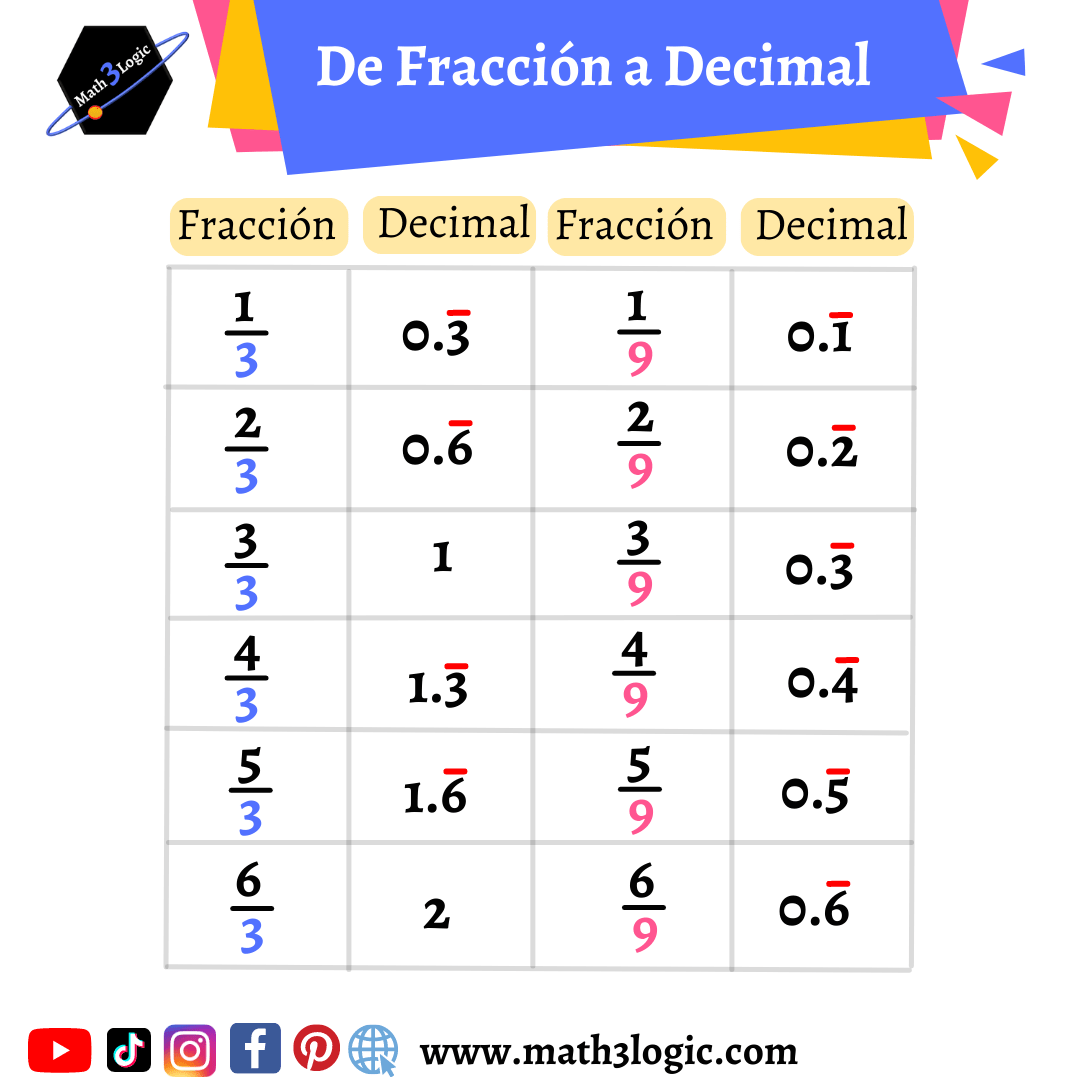
Nota: Puedes apoyarte con algunas de estás fracciones para convertirlas a su valor decimal sin la necesidad de realizar una división. Observa la tabla.
| Fracción | Decimal |
|---|---|
| 1/3 | 0.33... |
| 2/3 | 0.66... |
| 3/3 | 1 |
| 4/3 | 1.33... |
| 5/3 | 1.66... |
| 6/3 | 2 |
| 7/3 | 2.33... |
| 8/3 | 2.66... |
| 9/3 | 3 |
| Fracción | Decimal |
|---|---|
| 1/9 | 0.11... |
| 2/9 | 0.22... |
| 3/9 | 0.33... |
| 4/9 | 0.44... |
| 5/9 | 0.55... |
| 6/9 | 0.66... |
| 7/9 | 0.77... |
| 8/9 | 0.88... |
| 9/9 | 1 |
4.- Fracciones con valor decimal periódico mixto
Son aquellas que tienen una parte no periódica seguida de una parte periódica en la parte decimal.
Ejemplo
5/6 = 0.8333 … = 0.83̅
37/90 = 0.4111… = 0.41̅
7/12 = 0.5838383… = 0.58̅3̅
Fracciones menores, mayores e iguales a la unidad.
¡Recuerda!
Las fracciones propias son menores a la unidad, es decir, el valor numérico es menor a 1. En estas fracciones el numerador es menor que el denominador 3/5.
Las fracciones impropias son mayores a la unidad, es decir, el valor numérico es mayor a 1. En estas fracciones el numerador es mayor al denominador 7/4.
Las fracciones iguales a la unidad son aquellas que tanto el numerador como el denominador son iguales 8/8.
Las fracciones impropias se pueden representar como fracciones mixtas y las fracciones mixtas como fracciones impropias.
Las fracciones mixtas (simplificadas) se componen de una parte entera y una fracción propias. La parte entera y la fracción propia forman una representación completa y precisa de la cantidad total. La parte entera muestra cuántas unidades completas tienes (entero), mientras que la fracción propia captura la parte no entera de la cantidad (parte decimal), en forma de fracción.
Puedes repasar estos temas
Fracciones propias e impropias.
Convertir una fracción mixta en decimal
Como se mencionó previamente, las fracciones mixtas están compuestas por el entero y una fracción propia, por lo que es muy sencillo obtener su valor decimal.
Ejemplo 1
Solo divide la fracción propia para obtener el valor decimal y agregarlo al número entero.
2 enteros 1/4 = 2 + 1/4 = 2 + 0.25 = 2.25
5 enteros 3/5 = 5 + 3/5 = 5 + 0.6 = 5.6
1 entero 1/2 = 1 + 1/2 = 1 + 0.5 = 1.5
Otro método para obtener el valor decimal de una fracción mixta es convertirla en impropia para después dividir.
Ejemplo 2
2 enteros 1 /4 = 9/4 = 9 ÷ 4 = 2.25
5 enteros 3/5 = 28/5 = 28 ÷ 5 = 5.6
1 entero 1/2 = 3/2 = 3 ÷ 2 = 1.5
Galería de imágenes
En Math3logic se ha invertido mucho esfuerzo y dedicación en la creación de las imágenes. Si decides compartir el material, te pido amablemente que mantengas intacto el logo y todo lo que representa a Math3logic. Gracias 💙
Puedes guardar las imágenes en tus dispositivos 🖥️📱
Ejemplos- Convertir fracciones a decimales
| Fracción | Decimal |
|---|---|
| 1/2 | 0.50 |
| 2/2 | 1 |
| 3/2 | 1.50 |
| 4/2 | 2 |
| 5/2 | 2.5 |
| 6/2 | 3 |
| 7/2 | 3.5 |
| 8/2 | 4 |
| 9/2 | 4.5 |
| Fracción | Decimal |
|---|---|
| 1/3 | 0.33... |
| 2/3 | 0.66... |
| 3/3 | 1 |
| 4/3 | 1.33... |
| 5/3 | 1.66... |
| 6/3 | 2 |
| 7/3 | 2.33... |
| 8/3 | 2.66... |
| 9/3 | 3 |
| Fracción | Decimal |
|---|---|
| 1/4 | 0.25 |
| 2/4 | 0.50 |
| 3/4 | 0.75 |
| 4/4 | 1 |
| 5/4 | 1.25 |
| 6/4 | 1.50 |
| 7/4 | 1.75 |
| 8/4 | 2 |
| 9/4 | 2.25 |
| Fracción | Decimal |
|---|---|
| 1/5 | 0.2 |
| 2/5 | 0.4 |
| 3/5 | 0.6 |
| 4/5 | 0.8 |
| 5/5 | 1 |
| 6/5 | 1.2 |
| 7/5 | 1.4 |
| 8/5 | 1.6 |
| 9/5 | 1.8 |
| Fracción | Decimal |
|---|---|
| 1/6 | 0.166... |
| 2/6 | 0.33... |
| 3/6 | 0.50 |
| 4/6 | 0.66... |
| 5/6 | 0.833... |
| 6/6 | 1 |
| 7/6 | 1.166... |
| 8/6 | 1.33... |
| 9/6 | 1.50 |
| Fracción | Decimal |
|---|---|
| 1/8 | 0.125 |
| 2/8 | 0.25 |
| 3/8 | 0.375 |
| 4/8 | 0.50 |
| 5/8 | 0.625 |
| 6/8 | 0.75 |
| 7/8 | 0.875 |
| 8/8 | 1 |
| 9/8 | 1.125 |
| Fracción | Decimal |
|---|---|
| 1/9 | 0.11... |
| 2/9 | 0.22... |
| 3/9 | 0.33... |
| 4/9 | 0.44... |
| 5/9 | 0.55... |
| 6/9 | 0.66... |
| 7/9 | 0.77... |
| 8/9 | 0.88... |
| 9/9 | 1 |
| Fracción | Decimal |
|---|---|
| 1/10 | 0.1 |
| 2/10 | 0.2 |
| 3/10 | 0.3 |
| 4/10 | 0.4 |
| 5/10 | 0.5 |
| 6/10 | 0.6 |
| 7/10 | 0.7 |
| 8/10 | 0.8 |
| 9/10 | 0.9 |
Ejercicios – De Fracción a Decimal
Resuelve y ve si tu respuesta es correcta
Convierte la fracción en número decimal
Convierte la fracción en número decimal
Convierte la fracción en número decimal
Convierte la fracción en número decimal
Convierte la fracción en número decimal
Convierte la fracción en número decimal
Escoge la respuesta que consideres correcta
Convierte la fracción mixta en número decimal
Convierte la fracción mixta en número decimal
Convierte la fracción mixta en número decimal
¿Cuál es el valor decimal de la fracción?
Resuelve las operaciones y luego selecciona para ver la respuesta
Procura convertir cada fracción a decimal sin hacer ninguna operación. (Usando solo conocimientos previos)
Procura convertir cada fracción mixta a decimal sin hacer ninguna operación. (Usando solo conocimientos previos)
Termina la división y selecciona la respuesta correcta
¿Cuál es el resultado final?
¿Cuál es el resultado final?
¿Cuál es el resultado final?
Sigue practicando de fracciones a decimales
¡Prepárate para un desafío intelectual! Inicia el cuestionario.👨🏻🚀🚀🪐
💙Gracias a los anuncios, puedo seguir compartiendo todo lo que te gusta de Math3Logic. ¡Agradezco tu apoyo!
💙Recuerda que puedes encontrar todos los temas aquí Math3logic-Matemáticas. Si no encuentras alguno, ¡pronto lo tendrás disponible ahí mismo!
💙Si algo en la página no funciona o un enlace no se abre, por favor repórtalo por WhatsApp.
💙Recuerden que juntos hacemos un gran equipo 😊🧠💪🏻
Recuerda que en otros países el punto (.) se representa como una coma (,)
Más temas relacionados
Practicar otros temas
⭐ ¿Te sirvió la información?
Interacción con los anuncios
Quiero disculparme por los anuncios en la página que pueden afectar tu experiencia en Math3logic. Sin embargo, estos anuncios son una forma de apoyarme para que el sitio web pueda seguir creciendo. Si encuentras algún anuncio que te resulte interesante, puedes explorar la información que ofrece
Suscríbete a mi canal de YouTube
Si alguno de los vídeos de la página te resultó útil, sería de gran ayuda que te suscribieras a mi canal de YouTube, dejaras tu comentario o simplemente le dieras ‘me gusta’ al vídeo. Tu apoyo en estas acciones contribuye enormemente al crecimiento del canal y me anima a seguir compartiendo contenido útil
Sígueme e interactúa en mis redes sociales
Tu apoyo es invaluable cuando interactúas con mis publicaciones en redes sociales como Facebook, Instagram, TikTok, YouTube, y más. Agradezco mucho tu participación en estas plataformas.
¿Necesitas apoyo con algún tema de Math3logic?
Si después de ver el material de la página de Math3logic sobre algún tema aún tienes dudas entonces puedes enviarme un mensaje por WhatsApp para apoyarte.