Mínimo Común Múltiplo
Existen 3 diferentes métodos para encontrar el mínimo común múltiplo
1.- Utilizando los múltiplos de cada número. Como su nombre lo indica, identificas los múltiplos de cada número, seleccionas aquellos que son comunes entre ellos y eliges el menor de esos múltiplos; de ahí el nombre mínimo común múltiplo.
2.- Descomponiendo simultáneamente los números.
3.- Descomponiendo cada uno de los números por separado en factores primos.
Cada uno de los procedimientos es explicado paso a paso en los videos e imágenes de esta sección.
¿Qué son los múltiplos de un número?
Los múltiplos de un número son todos los números obtenidos (resultados) de multiplicar el número por los números naturales.
Ejemplos de múltiplos de 8.
8 x 1 = 8
8 x 2 = 16
8 x 3 = 24
8 x 4 = 32
8 x 5 = 40
Es así como algunos múltiplos de 8 son:
M8= {8, 16, 24, 32, 40 …}
1.- Mínimo Común Múltiplo de 2 números (mediante los múltiplos de cada número)
El mínimo común múltiplo de dos o más números es el número más pequeño de todos los múltiplos que tienen en común.
Existen dos formas para obtener el mínimo común múltiplo, también conocido como MCM. La primera forma recomiendo que se aplique solo para comprender el tema ya que se usa más cuando se trabajas con números pequeños. La segunda forma es para números más grandes y para que el procedimiento sea más rápido.
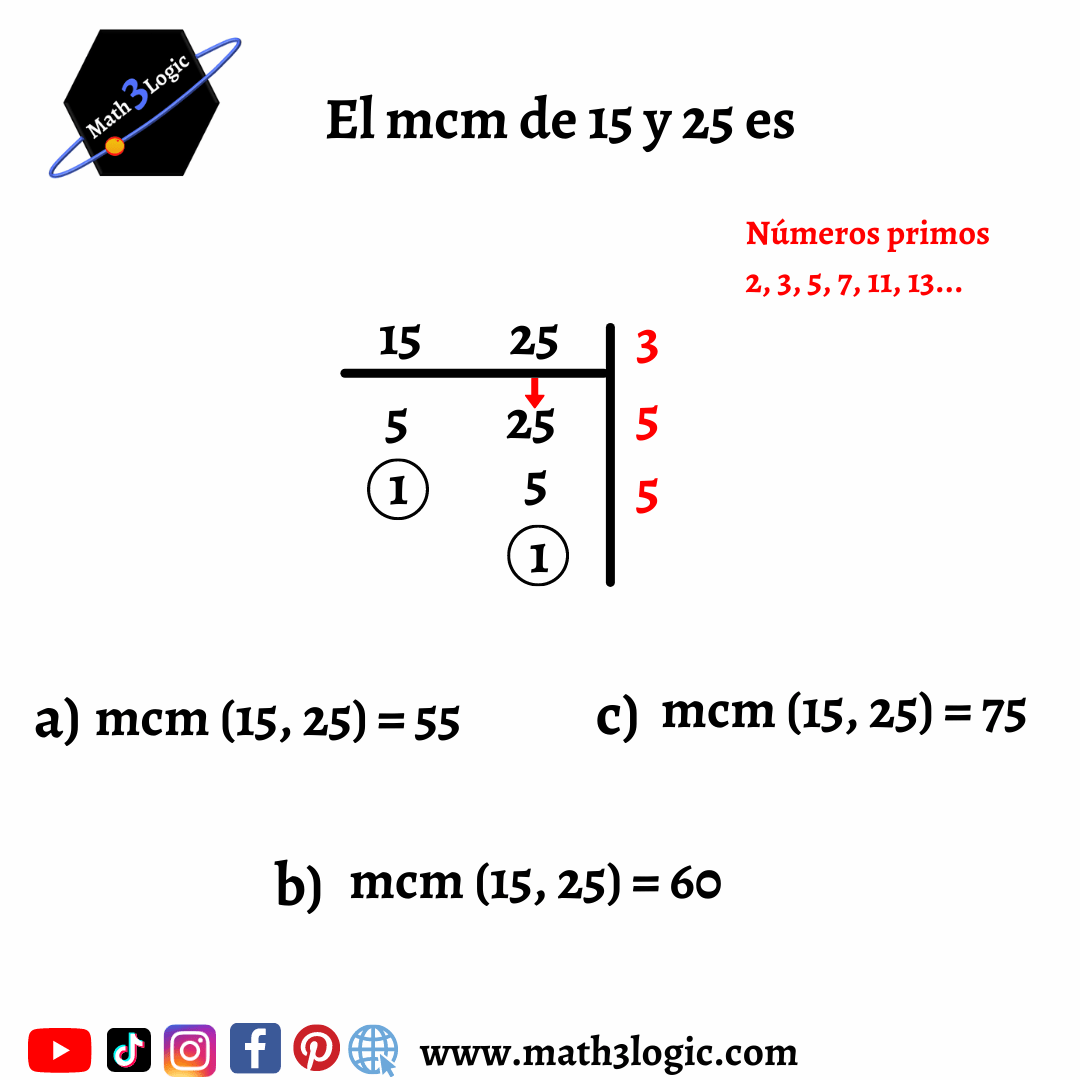
Encontrar el MCM (2, 3).
Paso 1.- Encontrar los múltiplos de 2 y de 3

Paso 2 .– Seleccionar los múltiplos en común.

Paso 3 .- Se toma el menor de todos los múltiplos.

Por lo tanto MCM (2, 3) = 6. El mínimo común múltiplo de 2 y 3 es 6.
Mínimo Común Múltiplo de 3 números
El procedimiento para calcular el MCM de tres números es exactamente el mismo que el anterior.
Encontrar el MCM (2, 3, 4).
Paso 1.- Encontrar los múltiplos de 2, 3 y 4

Paso 2 .– Seleccionar los múltiplos en común

Paso 3 .- Se toma el menor de todos los múltiplos

Por lo tanto MCM (2, 3, 4 ) = 12. El mínimo común múltiplo de 2, 3 y 4 es 12.
2.- Mínimo Común Múltiplo (descomponiendo simultáneamente los números en factores primos)
Para una mejor comprensión del mínimo común múltiplo, utilizando la descomposición en factores primos, te recomiendo repases los siguientes temas.
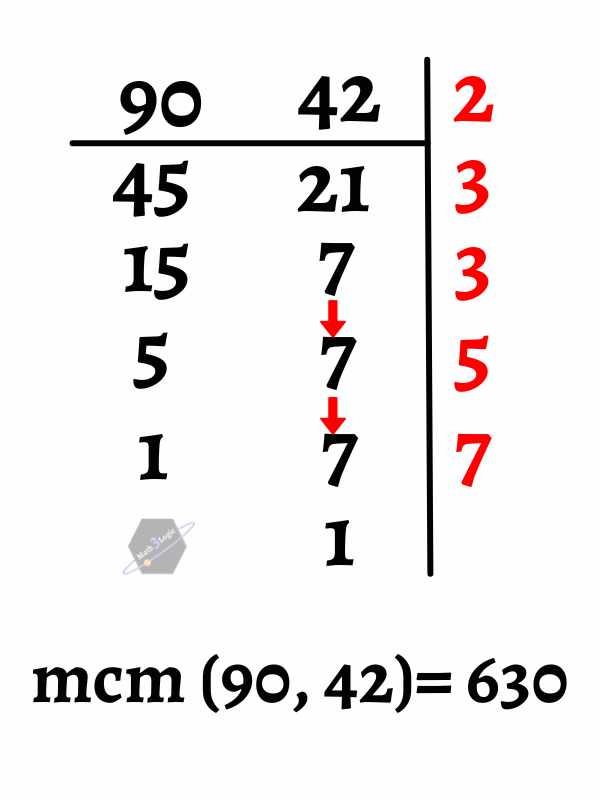
La forma más fácil y rápida de obtener el mínimo común múltiplo es a través de la descomposición simultánea de los números en sus factores primos. Luego, se multiplican los factores primos para obtener el MCM.
Por ejemplo, en la siguiente imagen, el mínimo común múltiplo de 90 y 42 es 2 × 3 × 3 × 5 × 7 = 360.
Uso del mínimo común múltiplo
El mínimo común múltiplo puede ser aplicado en diferentes temas, entre ellos:
Suma y resta de fracciones: Una manera de sumar dos o más fracciones (o fracciones mixtas) es encontrar el MCM de los denominadores, también conocido como mínimo común denominador. Luego, se busca una fracción equivalente para cada una de ellas, pero ahora con el mismo denominador, facilitando así la suma y resta de dos o más fracciones.
Comparación de fracciones: Hay varias formas de comparar fracciones, una de ellas consiste en hallar el MCM de los denominadores. Posteriormente, se obtienen fracciones equivalentes con el mismo denominador, lo que facilita la comparación final.
Localizar fracciones en una recta: Si necesitas ubicar más de dos fracciones en una recta, se recomienda seguir el mismo procedimiento que en casos anteriores: encontrar el MCM de los denominadores, obtener fracciones equivalentes para cada una de ellas, pero ahora con el mismo denominador. Finalmente, podrás ubicarlas en la misma recta.
Puedes observar que al trabajar con fracciones, resulta más sencillo cuando estas comparten el mismo denominador. Es ahí donde se hace necesario utilizar el MCM, especialmente al trabajar con más de dos fracciones.
Resolviendo problemas aplicando el MCM
Es frecuente que los alumnos no identifiquen fácilmente si un problema se resuelve utilizando el MCM o no. Por este motivo, decidí crear una sección específica para conocer las características más comunes de estos problemas.
Galería de imágenes
En Math3logic se ha invertido mucho esfuerzo y dedicación en la creación de las imágenes. Si decides compartir el material, te pido amablemente que mantengas intacto el logo y todo lo que representa a Math3logic. Gracias 💙
Otro manera de calcular el MCM
Problemas resueltos aplicando el MCM
Puedes guardar las imágenes en tus dispositivos 🖥️📱
Ejercicios – Mínimo Común Múltiplo
Encuentra el MCM de los siguientes números
El MCM de 3 y 5 es

El MCM de 4, 6 y 8 es

¡Prepárate para un desafío intelectual! Inicia el cuestionario.👨🏻🚀🚀🪐
Encuentra el MCM de los siguientes números
El MCM de 60 y 72 es
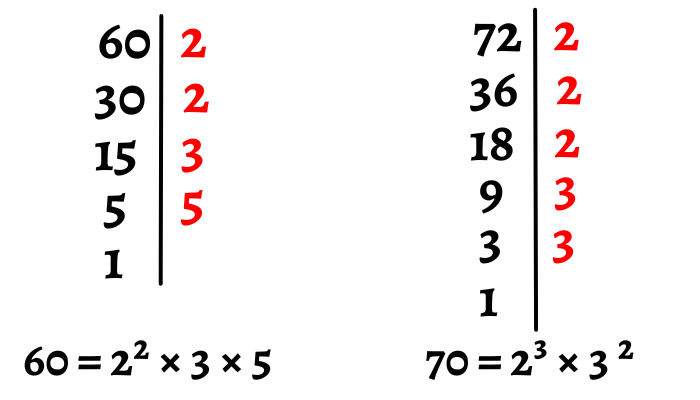
El MCM de 42 y 45 es

El MCM de 20, 35 y 54 es

El MCM de 12, 18 y 24 es
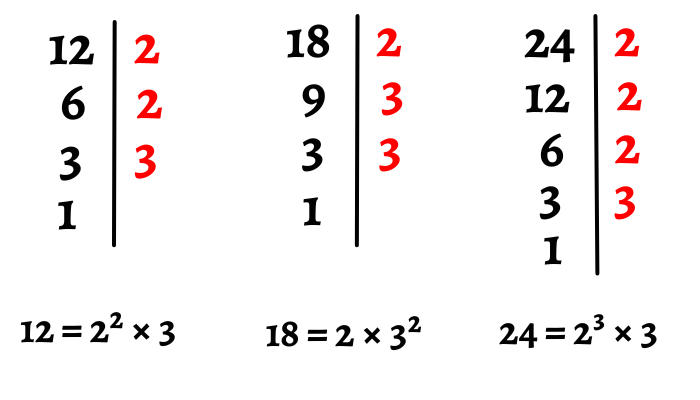
¡Prepárate para un desafío intelectual! Inicia el cuestionario.👨🏻🚀🚀🪐
Encuentra el MCM de los siguientes números
El MCM de 4 y 10 es

El MCM de 7 y 11 es

El MCM de 14, 18 y 20 es es
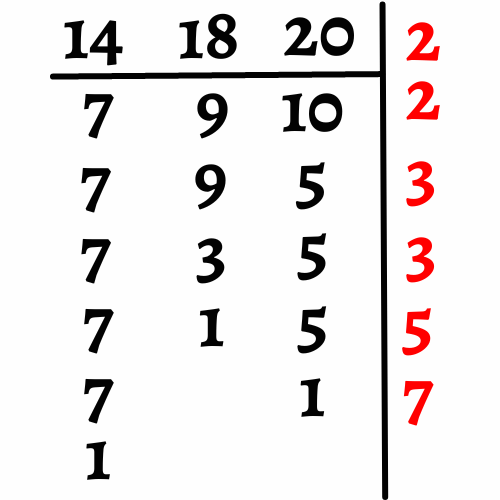
Identifica los valores de los cuales se obtuvo el mínimo común múltiplo
8 es el MCM de
78 es el MCM de
140 es el MCM de
Calcular el MCM de dos números.
Introduce los números que quieres calcular
(Sólo números naturales, si insertas decimales tomará encuenta solo la parte entera)
🧠Comprueba tus conocimientos
Sigue practicando mínimo común múltiplo
💙Gracias a los anuncios, puedo seguir compartiendo todo lo que te gusta de Math3Logic. ¡Agradezco tu apoyo!
💙Recuerda que puedes encontrar todos los temas aquí Math3logic-Matemáticas. Si no encuentras alguno, ¡pronto lo tendrás disponible ahí mismo!
💙Si algo en la página no funciona o un enlace no se abre, por favor repórtalo por WhatsApp.
💙Recuerden que juntos hacemos un gran equipo 😊🧠💪🏻
Más temas relacionados
Practicar otros temas
⭐ ¿Te sirvió la información?
Interacción con los anuncios
Quiero disculparme por los anuncios en la página que pueden afectar tu experiencia en Math3logic. Sin embargo, estos anuncios son una forma de apoyarme para que el sitio web pueda seguir creciendo. Si encuentras algún anuncio que te resulte interesante, puedes explorar la información que ofrece
Suscríbete a mi canal de YouTube
Si alguno de los vídeos de la página te resultó útil, sería de gran ayuda que te suscribieras a mi canal de YouTube, dejaras tu comentario o simplemente le dieras ‘me gusta’ al vídeo. Tu apoyo en estas acciones contribuye enormemente al crecimiento del canal y me anima a seguir compartiendo contenido útil
Sígueme e interactúa en mis redes sociales
Tu apoyo es invaluable cuando interactúas con mis publicaciones en redes sociales como Facebook, Instagram, TikTok, YouTube, y más. Agradezco mucho tu participación en estas plataformas.
¿Necesitas apoyo con algún tema de Math3logic?
Si después de ver el material de la página de Math3logic sobre algún tema aún tienes dudas entonces puedes enviarme un mensaje por WhatsApp para apoyarte.