Máximo Común Divisor
Existen 3 diferentes métodos para encontrar el máximo común divisor
1.- Utilizando los divisores de cada número. Como su nombre lo indica, se identifican los divisores de cada número, se seleccionan los divisores comunes y se elige el mayor de ellos; de ahí el nombre máximo común divisor.
2.- Descomponiendo cada número por separado en factores primos. Se descompone cada número en sus factores primos, luego se toman los factores primos comunes con el menor exponente de cada número. El producto de todos esos factores es el MCD.
3.- Descomponiendo simultáneamente los números. Los números se descomponen en factores primos al mismo tiempo. El producto de estos factores es el MCD.
Cada uno de los procedimientos es explicado paso a paso en los videos e imágenes de esta sección.
¿Qué son los divisores de un número?
Los divisores de un número son todos los números naturales que entran una cantidad exacta de veces en él sin que sobre nada.
Ejemplo de divisores de 12.
12 ÷ 1 = 12
12 ÷ 2 = 6
12 ÷ 3 = 4
12 ÷ 4 = 3
12 ÷ 6 = 2
12 ÷ 12 = 1
Es así como los divisores de 12 son:
D12= {1, 2, 3, 4, 6, 12}
Método 1 – Máximo común divisor
(mediante sus divisores)
Máximo Común Divisor de dos números (mediante los divisores de cada número)
El Máximo Común Divisor de dos o más números es el número más grande de todos los divisores que tienen en común.
Ejemplo: Encontrar el MCD (12, 18)
Paso 1.- Encontrar los divisores de 12 y 18.

Paso 2 .– Seleccionar los divisores en común

Paso 3 .- Se toma el mayor de los divisores.

Por lo tanto, el máximo común divisor de 12 y 18 es 6.
MCD (12, 18) = 6
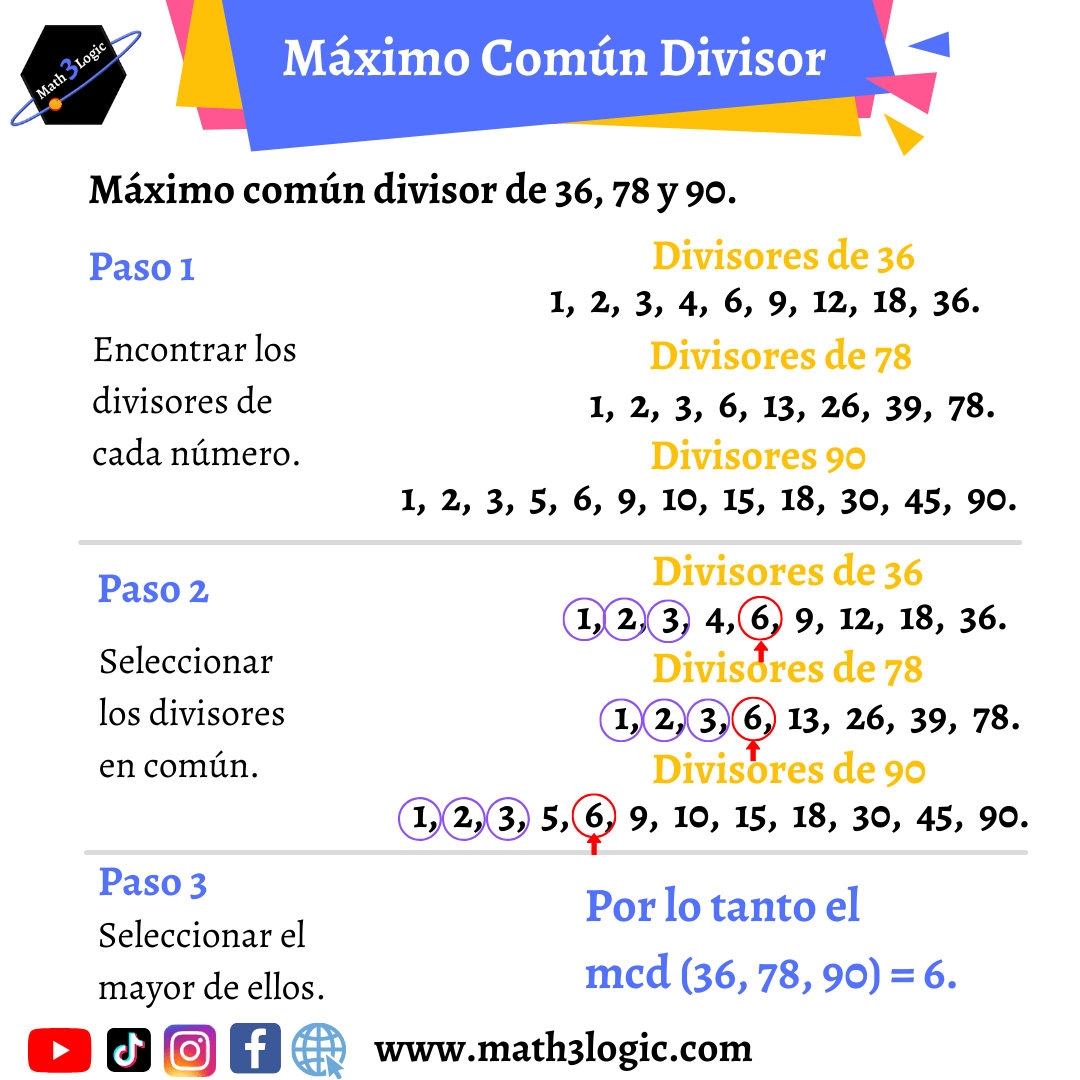
Máximo común divisor de 3 números
El procedimiento para calcular el MCD de tres números es exactamente el mismo que el anterior.
Ejemplo: Encontrar el MCD (42, 70, 154).
Paso 1.- Encontrar los divisores de 42, 70 y 154.

Paso 2 .– Seleccionar los divisores en común

Paso 3 .- Se toma el mayor de los divisores.

Por lo tanto, el máximo común divisor de 42, 70 y 156 es 14.
MCD (42, 70, 156) = 14
Método 2 – Máximo común divisor
(mediante la descomposición en factores primos)
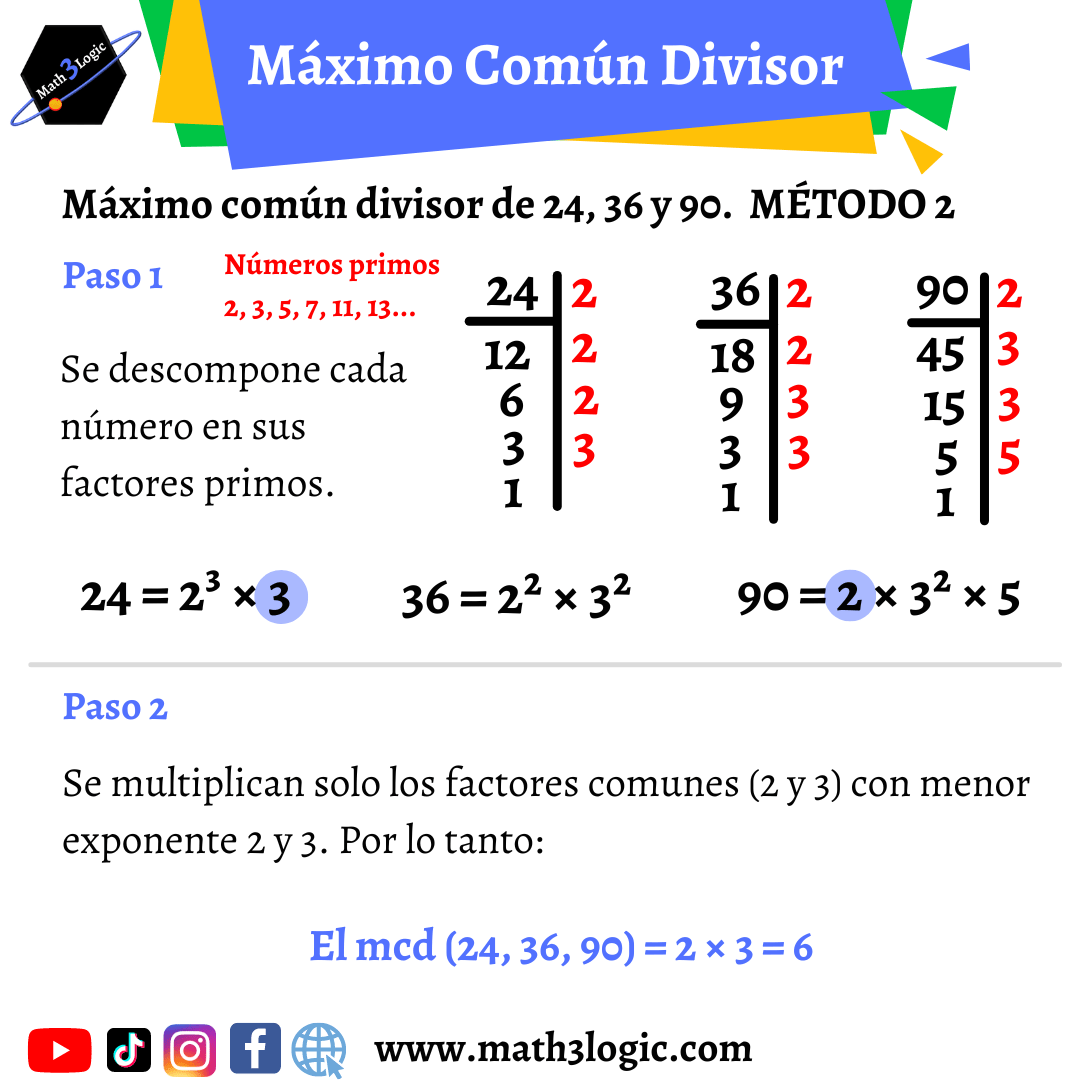
Máximo Común Divisor (descomponiendo cada numero por separado en factores primos)
Para una mejor comprensión del máximo común divisor usando la descomposición en factores primos te recomiendo repases los siguientes temas.
Ejemplo: Encontrar el MCD(210, 350).
Paso 1.- Se descompone cada número en factores primos.
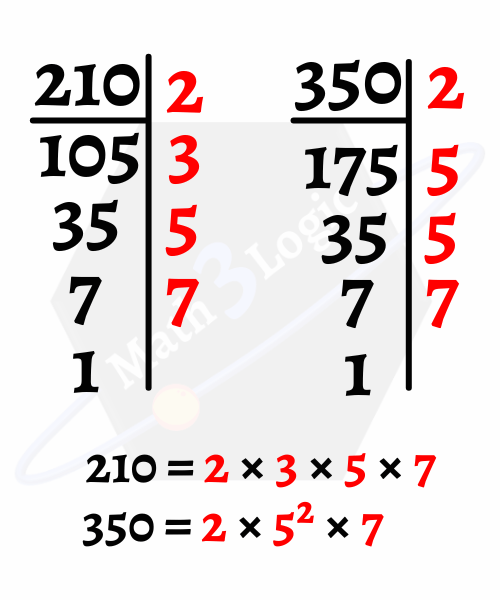
Paso 2.- Se multiplican solo los factores primos comunes con menor exponente (2, 5 y 7). Por lo tanto, el máximo común divisor de 210 y 350 es 70.
MCD(210, 350) = 2 × 5 × 7 = 70
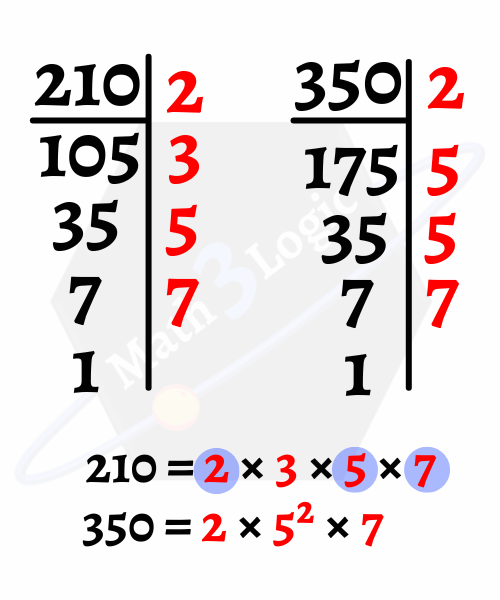
Ejemplo: Encontrar el MCD(54, 90, 126).
Paso 1.- Se descompone cada número en factores primos.
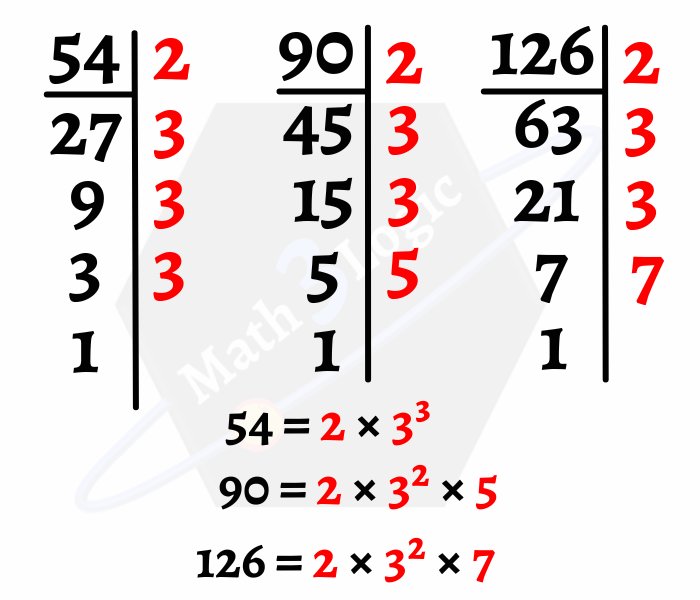
Paso 2.- Se multiplican solo los factores primos comunes con menor exponente (2 y 3²). Por lo tanto, el máximo común divisor de 54, 90 y 126 es 18
MCD(54, 90, 126) = 2 × 3² = 18

Método 3 – Máximo común divisor
(mediante descomposición simultánea)
Máximo Común Divisor (descomponiendo sumultáneamente los números en factores primos)
Para una mejor comprensión del máximo común divisor usando la descomposición en factores primos te recomiendo repases los siguientes temas.
La descomposición simultánea para hallar el máximo común divisor (MCD) de dos números consiste en descomponer ambos números en sus factores primos al mismo tiempo. Cada número se coloca en una columna, y a la derecha se van dividiendo por los factores primos que dividan exactamente a ambos números. Se comienza con el factor primo más pequeño (2) y se continúa con los siguientes (3, 5, 7, etc.), deteniéndose cuando ninguno de los dos números sea divisible por un mismo número primo. El MCD es el producto de todos los factores primos comunes utilizados en las divisiones.
Ejemplo: Encontrar el MCD(210, 350.)
Paso 1.- Se descomponen simultáneamente los dos números.

Paso 2.- Se multiplican todos los factores primos obtenidos 2 × 5 × 7. Por lo tanto, el máximo común divisor de 210 y 350 es 70.
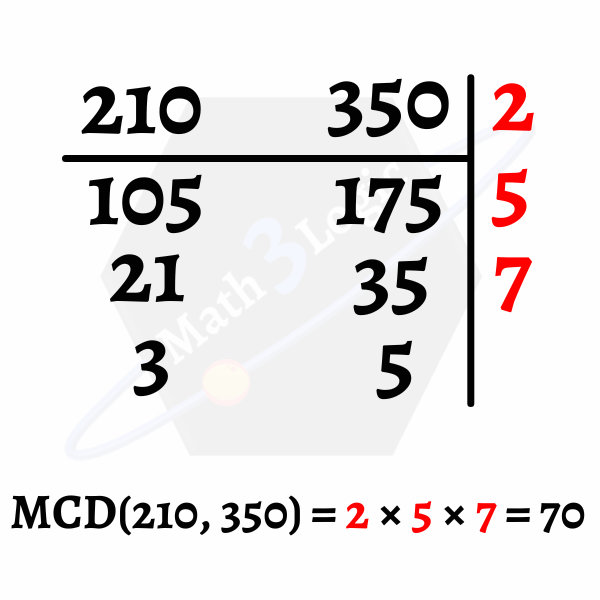
Ejemplo: Encontrar el MCD(54, 90, 126).
Paso 1.- Se descomponen simultáneamente los tres números.

Paso 2.- Se multiplican todos los factores primos obtenidos 2 × 3². Por lo tanto, el máximo común divisor de 54, 90 y 126 es 18.

Todos los métodos en video y sus aplicaciones del máximo común divisor
Resolviendo problemas aplicando el MCD
Es muy común que los alumnos no identifiquen fácilmente si un problema se resuelve usando el mcd o no, por ese motivo decidí hacer una sección especifica para saber las características más comunes que tiene estos problemas.
Galería de Imágenes
En Math3logic®️me esfuerzo por crear material divertido y útil para ti🥰. Si decides descargarlo/compartirlo, te pido por favor que dejes el logo intacto y todo lo que representa a Math3logic©️ . También, te agradecería mucho si no modificas las imágenes ni las subes a otros sitios web. ¡Gracias por preferirme y por apoyar el trabajo que hago! 💙
Problemas resueltos aplicando el MCD
Puedes guardar las imágenes en tus dispositivos 🖥️📱
Ejercicios – Máximo Común Divisor
Selecciona el método que deseas practicar
Método 1 - MCD Mediante sus divisores
Método 2 - MCD Descomponiendo en factores primos
Método 3 - MCD Descomposición simultánea
💙Si algo en la página no funciona o un enlace no se abre, por favor repórtalo por WhatsApp.
💙Si descargas/ compartes las imágenes, por favor mantén el logo y todo lo que representa Math3logic©️®️ .
💙Gracias a los anuncios, puedo seguir compartiendo todo lo que te gusta de Math3Logic. ¡Agradezco tu apoyo!
💙Recuerda que puedes encontrar todos los temas aquí Math3logic-Matemáticas. Si no encuentras alguno, ¡pronto lo tendrás disponible ahí mismo!
💙Recuerden que juntos hacemos un gran equipo 😊🧠💪🏻
Comprueba tus conocimientos🧠
Calcular el MCD de dos números.
Introduce los números que quieres calcular
(Sólo números naturales, si insertas decimales tomará encuenta solo la parte entera)
Calcular el MCD de tres números.
Introduce los números que quieres calcular
(Sólo números naturales, si insertas decimales tomará encuenta solo la parte entera)
✨Temas relacionados
Practicar otros temas
⭐ ¿Te sirvió la información?
Suscríbete a mi canal de YouTube
Si alguno de los vídeos de la página te resultó útil, sería de gran ayuda que te suscribieras a mi canal de YouTube, dejaras tu comentario o simplemente le dieras ‘me gusta’ al vídeo. Tu apoyo en estas acciones contribuye enormemente al crecimiento del canal y me anima a seguir compartiendo contenido útil
Wishlist de Math3logic - Pequeños Gustos, Gran Inspiración
Tu apoyo significa el mundo para mí. Esta Wishlist de Amazon incluye pequeños detalles y artículos que me inspiran a seguir creando material educativo de calidad para mis estudiantes. ¡Gracias por ser parte de esta aventura matemática!
Interacción con los anuncios
Quiero disculparme por los anuncios en la página que pueden afectar tu experiencia en Math3logic. Sin embargo, estos anuncios son una forma de apoyarme para que el sitio web pueda seguir creciendo. Si encuentras algún anuncio que te resulte interesante, puedes explorar la información que ofrece
Clases particulares en línea
Antes de unirte, ten en cuenta que estas clases no se enfocan en un solo tema aislado. Para llegar al contenido que necesitas, es fundamental comprender las bases primero. ¡Aprender matemáticas es un proceso, y estoy aquí para guiarte en cada paso!
¡Agenda una clase muestra gratis y comienza tu aprendizaje!