Números Primos y Compuestos
Números Naturales
El conjunto de números naturales, denotado como:
N = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 … },
está compuesto por:
- El número 1, que no es primo ni compuesto.
- Los números primos: 2, 3, 5, 7, 11, 13, 17 …
- Los números compuestos: 4, 6, 8, 9, 10 ,12, 14, 15…
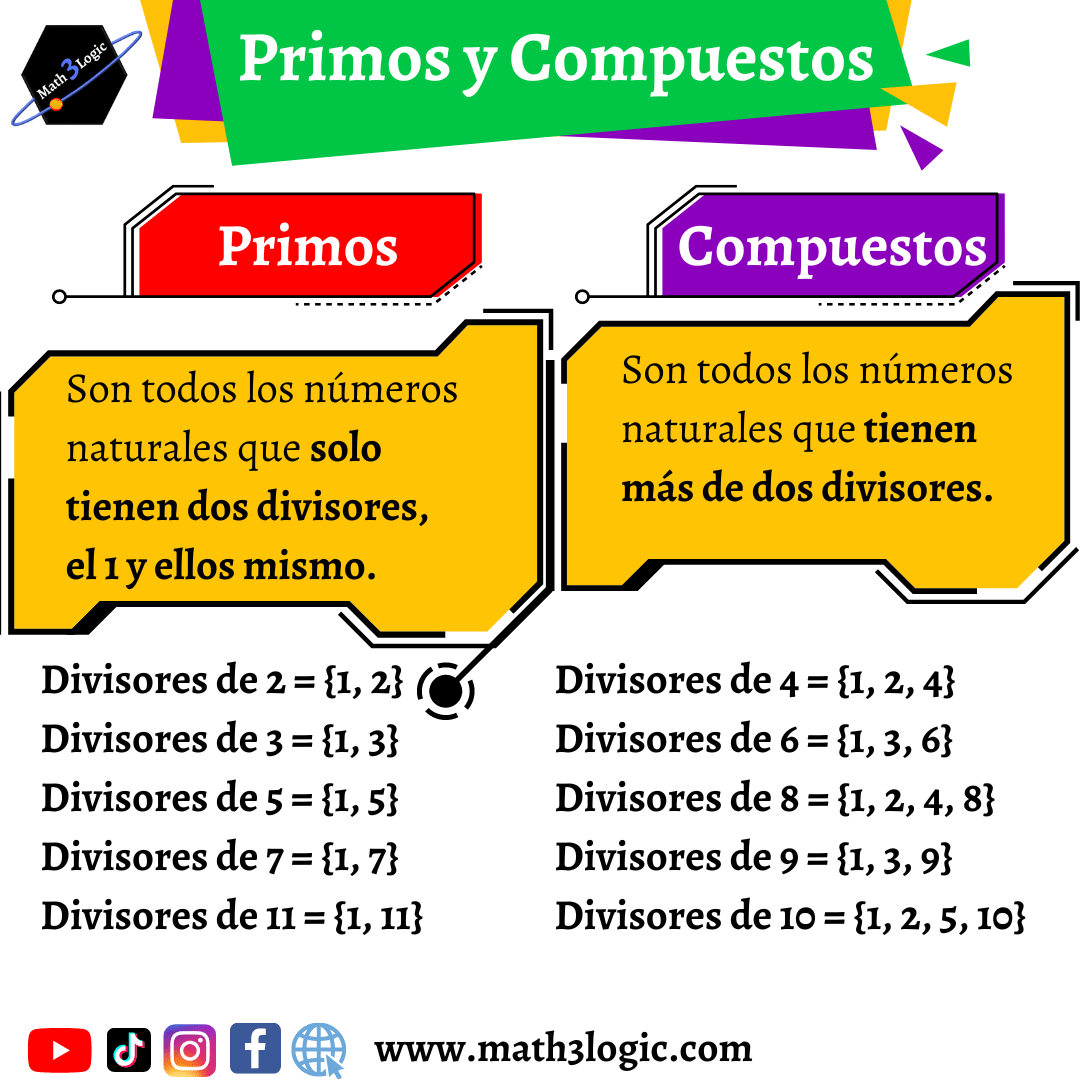
Números Primos
Los números primos son aquellos números naturales que tienen exactamente dos divisores: el uno y ellos mismo. Por ejemplo:
Divisores de 2 = {1, 2}
Divisores de 3 = {1, 3}
Divisores de 5 = {1, 5}
Divisores de 7 = {1, 7}
Divisores de 11 = {1, 11}
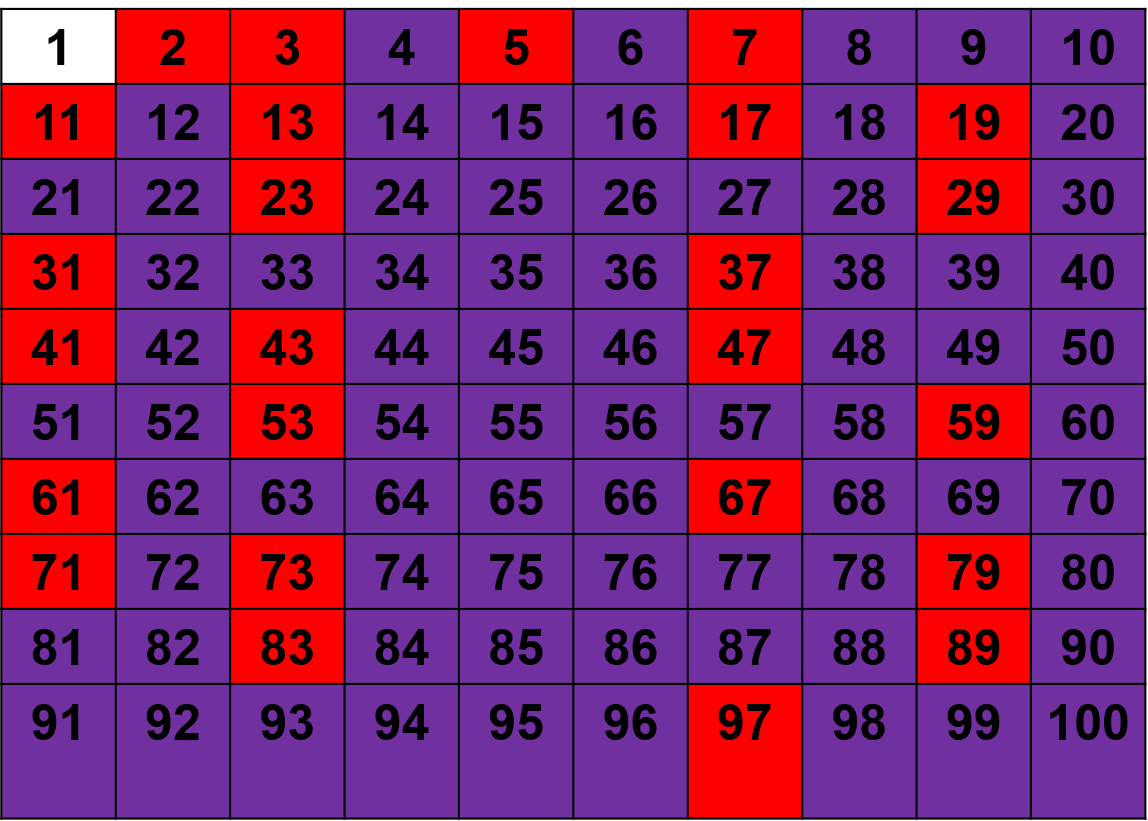
En la tabla a continuación, los números resaltados en rojo son todos primos.
Números Compuestos
Los números compuestos son aquellos números naturales que tienen más de dos divisores. Por ejemplo:
Divisores de 4 = {1, 2, 4}
Divisores de 6 = {1, 2, 3, 6}
Divisores de 8 = {1, 2, 4, 8}
Divisores de 9 = {1, 3, 9}
Divisores de 10 = {1, 2, 5, 10}
En la tabla siguiente los números resaltados de morado son todos compuestos.
Primos y Compuestos
Uso de los números primos
La multiplicación de números primos como 2, 3, 5, 7, entre otros, generan números compuestos como 4, 6, 8, 9, entre otros.
Ejemplos:
2 × 5 = 10
3 × 7 = 21
Los números naturales N = {1, 2, 3, 4, 5, 6, 7, 8, 9 …} se componen del 1, los números primos y los compuestos (productos de primos). Por lo tanto, los números primos pueden ser usados en diversos temas.
Factores primos: Para descomponer un número en sus factores primos, es necesario saber cuáles son los números primos y comprender su diferencia con los números compuestos.
Mínimo común múltiplo: Encontrar el MCM de dos o más números se puede hacer de dos diferentes maneras; sin embargo, descomponer los números en sus factores primos es el más práctico, y para ello, es necesario tener en cuenta los números primos.
Máximo común divisor: Lo mismo ocurre al encontrar el MCD de dos o más números: es necesario descomponer los números en sus factores primos, para lo cual se requiere conocer los números primos.
Simplificación de fracciones: Puedes simplificar una fracción utilizando números primos y compuestos, sin embargo, al comprender el tema resulta más fácil hacerlo únicamente con números primos.
Criterios de Divisibilidad para saber si es compuesto
Los criterios de divisibilidad te permiten determinar fácilmente si un número es divisible por los números primos 2, 3 o 5. En caso de serlo, el número automáticamente se considera compuesto, ya que tendría más de dos divisores.
Ejemplos:
El número 46 es compuesto debido a que termina en número par. Esto indica que es divisible por 2, por lo que entre sus divisores se encuentran el 1, 2 y 46. Aunque tienen más divisores, con esos tres es suficiente para confirmar que es un número compuesto.
El número 175 es compuesto porque termina en cinco. Esto significa que es divisible por 5, entonces entre sus divisores se encuentran el 1, 5 y 75. Aunque tiene más divisores, con estos tres es suficiente para confirmar que es un número compuesto.
El número 51 es compuesto porque la suma de sus dígitos, 5 + 1, es igual a 6, y seis es múltiplo de 3. Eso significa que es divisible por 3 porque entre sus divisores se encuentran el 1, 3 y 51. Aunque tiene más divisores, con estos tres es suficiente para confirmar que es un número compuesto.
Nota: Recuerda que 2, 3 y 5 son primos, pero su producto, es decir, al multiplicarlos, se obtienen números compuestos.
Galería de imágenes
Puedes guardar las imágenes en tus dispositivos 🖥️📱
Ejemplos- Números primos y compuestos
| Número | Divisores | Primos |
|---|---|---|
| 2 | 1, 2 | P |
| 3 | 1, 3 | P |
| 5 | 1, 5 | P |
| 7 | 1, 7 | P |
| 11 | 1, 11 | P |
| 13 | 1, 13 | P |
| 17 | 1, 17 | P |
| 19 | 1, 19 | P |
| Número | Divisores | Compuesto |
|---|---|---|
| 4 | 1, 2, 4 | C |
| 6 | 1, 2, 3, 6 | C |
| 8 | 1, 2, 4, 8 | C |
| 9 | 1, 3, 9 | C |
| 10 | 1, 2, 5, 10 | C |
| 12 | 1, 2, 3, 4, 6, 12 | C |
| 14 | 1, 2, 7, 14 | C |
| 15 | 1, 3, 5, 15 | C |
| 16 | 1, 2, 4, 8, 16 | C |
| 18 | 1, 2, 3, 6, 9, 18 | C |
| 20 | 1, 2, 4, 5, 10, 20 | C |
Ejercicios – Números Primos y Compuestos
¿Primo o compuesto?
El número 51 es
El número 97 es
El número 91 es
El número 89 es
El número 77 es
Selecciona un número para ver si es primo o compuesto
Escribe un número y ve si es primo o compuesto.
(Recuerda insertar solo números naturales, si insertas decimales sólo tomará en cuenta el entero.)
🧠Comprueba tus conocimientos
Sigue practicando números primos y compuestos
¡Prepárate para un desafío intelectual! Inicia el cuestionario.👨🏻🚀🚀🪐
Más temas relacionados
Practicar otros temas
⭐ ¿Te sirvió la información?
Interacción con los anuncios
Quiero disculparme por los anuncios en la página que pueden afectar tu experiencia en Math3logic. Sin embargo, estos anuncios son una forma de apoyarme para que el sitio web pueda seguir creciendo. Si encuentras algún anuncio que te resulte interesante, puedes explorar la información que ofrece
Suscríbete a mi canal de YouTube
Si alguno de los vídeos de la página te resultó útil, sería de gran ayuda que te suscribieras a mi canal de YouTube, dejaras tu comentario o simplemente le dieras ‘me gusta’ al vídeo. Tu apoyo en estas acciones contribuye enormemente al crecimiento del canal y me anima a seguir compartiendo contenido útil
Sígueme e interactúa en mis redes sociales
Tu apoyo es invaluable cuando interactúas con mis publicaciones en redes sociales como Facebook, Instagram, TikTok, YouTube, y más. Agradezco mucho tu participación en estas plataformas.
¿Necesitas apoyo con algún tema de Math3logic?
Si después de ver el material de la página de Math3logic sobre algún tema aún tienes dudas entonces puedes enviarme un mensaje por WhatsApp para apoyarte.