Problemas de Mínimo Común Múltiplo
¿Cómo saber cuando usar el MCM para resolver un problema?
Para saber si un problema se resuelve usando el mínimo común múltiplo se debe analizar el contexto y los elementos del problema. El mcm regularmente se usa cuando deseas encontrar un momento en el que dos o más eventos ocurran simultáneamente, puedes usar el mcm de los dos períodos o tiempos en los que ocurren los eventos. Los problemas más comunes son cuando se involucran horarios y tiempos de encuentro.
Horarios y tiempos de encuentro: Si el problema pide calcular cuando dos personas u objetos (aviones, autobuses, etc.) se encontrarán después de realizar cierto acción (correr, volar, caminar, etc.) en intervalos de tiempo diferentes se puede utilizar el mcm de esos intervalos de tiempo para determinar el punto de encuentro.
También se aplica para ciclos repetitivos, sincronizar eventos y mucho más.
Preguntas que te pueden ayudar a determinar si tu problema se resuelve usando el MCM
¿El problema se relaciona con la longitud de ciclos o periodos repetitivos? Si el problema implica la medición de la longitud de ciclos, como el tiempo que tarda un objeto en dar una vuelta completa, o la repetición de un patrón, como el número de días que pasan hasta que se repita un fenómeno, el mcm puede ser utilizado para calcular esas longitudes.
¿El problema se refiere a la repetición o sincronización de eventos? Si el problema se relaciona con la ocurrencia de eventos en un ciclo o patrón, y se necesita determinar cuándo esos eventos se repetirán o coincidirán nuevamente, el mcm puede ser necesario.
¿Hay repartición equitativa o distribución de elementos en el problema? Si el problema involucra repartir o distribuir elementos de manera equitativa entre varias personas o grupos, y se busca determinar cuándo se repetirá exactamente la misma cantidad de elementos para cada uno, el mcm podría ser relevante.
¿El problema implica calcular el tiempo mínimo necesario para que dos o más eventos ocurran simultáneamente? Si necesitas determinar el instante en el que dos o más eventos sucederán al mismo tiempo, es probable que el mcm sea necesario para encontrar ese punto de coincidencia.
¿El problema se relaciona con horarios, calendarios o planificación? Si el problema implica la coordinación de horarios, el cálculo de intervalos de tiempo o la planificación de eventos periódicos, el mcm puede ser útil.
¿Se requiere determinar el número mínimo de repeticiones necesarias para que ocurra un evento específico? Si el problema requiere saber cuántas veces debe repetirse una acción o evento para que se cumpla una condición específica, el mcm puede ser utilizado para encontrar ese número mínimo.
Recuerda que estas pautas son solo indicativas y no abarcan todos los posibles casos. Al analizar el enunciado del problema, es importante comprender las relaciones y las necesidades específicas para determinar si el mcm es una herramienta adecuada para su resolución.
Problema 1
Se tiene una canción que se repite cada 2 minutos y otra canción que se repite cada 3 minutos. ¿Después de cuánto tiempo las dos canciones comenzarán desde el principio y al mismo tiempo?
Para determinar cuándo las dos canciones comenzarán desde el principio y al mismo tiempo, se necesita encontrar el mínimo común múltiplo (mcm) de los intervalos de tiempo en los que se repiten las canciones.
En este caso, una canción se repite cada 2 minutos y la otra cada 3 minutos. El mínimo común múltiplo de 2 y 3 es 6 (observa la imagen).
Por lo tanto, después de 6 minutos, las dos canciones comenzarán desde el principio y al mismo tiempo.

Problema 2
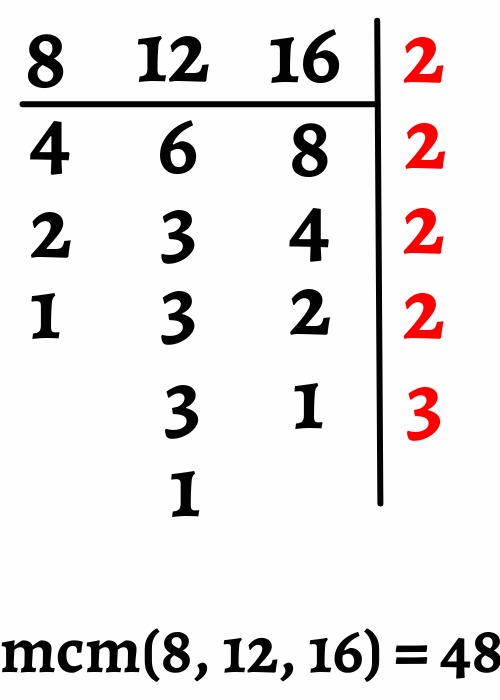
Una luz se enciende cada 8 segundos, otra luz se enciende cada 12 segundos y una tercera luz se enciende cada 16 segundos. ¿Después de cuántos segundos las tres luces se encenderán al mismo tiempo?
Para determinar después de cuántos segundos las tres luces se encenderán al mismo tiempo, se debe encontrar el mínimo común múltiplo (mcm) de los intervalos de encendido de las luces.
En este caso, las luces se encienden cada 8 segundos, 12 segundos y 16 segundos. El mínimo común múltiplo de 8, 12 y 16 es 48 (observa la imagen).
Por lo tanto, las tres luces se encenderán al mismo tiempo después de 48 segundos.
Problema 3
Tres atletas inician su entrenamiento a las 6: 00 am, el primero recorre la pista en 12 minutos, el segundo recorre la pista en 15 minutos y el tercero recorre la pista en 20 minutos. ¿A qué hora volverán a coincidir los tres atletas en el lugar de inicio?, ¿cuántas vueltas ha dado a la pista el primer atleta?¿cuántas el segundo atleta? y ¿cuántas el tercero?
Primero se calcula el mcm de los minutos en los que cada atleta recorre la pista, es decir, de 12, 15 y 20, el objetivo es saber en cuánto tiempo volverán a coincidir los tres atletas.
El mcm de 12, 15 y 20 es 60 (observa la imagen). Por lo que los atletas coinciden después de 60 minutos, es decir después de 1 hora. Por lo tanto volverán a coincidir a las 7:00 am.
Ahora para saber cuántas vueltas dio cada atleta se divide el mínimo común múltiplo entre los minutos que cada atleta hace en cada vuelta.
Primer atleta dio 60÷12 = 5 vueltas
Segundo atleta dio 60 ÷ 15 = 4 vueltas
Tercer atleta dio 60 ÷ 20 = 3 vueltas

Problema 4
Tres autobuses salen de la estación. El primer autobús recorre una ruta completa en 18 minutos, el segundo autobús en 24 minutos y el tercer autobús en 30 minutos. ¿Después de cuánto tiempo los tres autobuses se volverán a encontrar en la estación? ¿Cuántas vueltas completas dio cada autobús?
Primero se calcula el mcm de los tiempos de los autobuses, es decir, de 18, 24 y 30, esto nos da el tiempo mínimo necesario que hacen los autobuses para volverse a encontrar en la estación.
El mcm de 18, 24 y 30 es 360 (observa la imagen). Esto significa que cada 360 minutos los autobuses se encuentran en la estación, es decir, después de 360÷60 = 6 horas.
Ahora para saber cuántas vueltas dio cada autobús se divide el mínimo común múltiplo entre los minutos que hace cada autobús para llegar a la estación.
Primer autobús dio 360 ÷18 = 20 vueltas
Segundo autobús dio 360 ÷ 24 = 15 vueltas
Tercer autobús dio 360 ÷ 30 = 12 vueltas

Problemas sobre el máximo común divisor (MCD)
¿Cómo saber si tu problema se resuelve mediante el MCD?
Para entender si tu problema puede resolverse utilizando el máximo común divisor (MCD), revisa los casos específicos que se explican en el siguiente enlace. Ahí encontrarás una variedad de problemas que se abordan y se resuelven aplicando el concepto del MCD.
Galería de imágenes
En Math3logic se ha invertido mucho esfuerzo y dedicación en la creación de las imágenes. Si decides compartir el material, te pido amablemente que mantengas intacto el logo y todo lo que representa a Math3logic. Gracias 💙
Otro manera de calcular el MCM
Puedes guardar las imágenes en tus dispositivos 🖥️📱
Ejercicios – Problemas de MCM
Lee cada problema y selecciona la respueta correcta
Dos atletas corren diariamente a la misma hora, el primero tarda 10 minutos y el segundo tarda 14 minutos en dar una vuelta. ¿Después de cuánto minutos volverán a coincidir en el punto de partida?
Dos autobuses salen de su base a las 5:00 am; el primero regresa 80 minutos después y el segundo 120 minutos después, tiempo que utilizan para su recorrido. ¿A qué hora volverán a coincidir en la base de autobuses?
Tres galgos compiten en una carrera el primero tarda 30 segundos en dar una vuelta a la pista, el segundo tarda 45 segundo y el tercero 50 segundos. ¿Cuántas vueltas debe dar cada uno para que vuelvan a coincidir en el punto de partida?
Tres nadadores compiten en una piscina. El primer nadador tarda 40 segundos en dar una vuelta, el segundo nadador tarda 1 minuto y 10 segundos, y el tercer nadador tarda 1 minuto y 30 segundos en dar una vuelta. ¿Cuántas vueltas deben dar cada uno para que vuelvan a coincidir en el punto de partida?
Identifica si el problema se resuelve usando el MCM o no
Un cuerpo sano mantiene un equilibrio entre masa muslcular, grasa y huesos. Si un atleta pesa 70 kg y dice que tiene 14 kg de puro músculo. ¿Qué porcentaje de su masa total es de músculo?
Un paciente debe tomar tres medicamentos diferentes: A, B y C. El medicamento A se toma cada 4 horas, el medicamento B cada 6 horas y el medicamento C cada 8 horas. El paciente quiere saber cuántas veces al día coincidirán los horarios de toma de los tres medicamentos.
En una fábrica de fusibles se sabe que para cubrir un pedido en 24 días se necesitan 4 empleados que trabajen tiempo completo. ¿Cuántos empleados necesitarían para cubrir el mismo pedido en 6 días?
Un colegio organiza una excursión y tiene dos opciones de autobuses para transportar a los estudiantes. El primer autobús sale cada 30 minutos y el segundo autobús sale cada 40 minutos. Si los dos autobuses salen al mismo tiempo, ¿después de cuántos minutos se encontrarán nuevamente?
Un grupo de amigos quiere hacer ejercicio juntos en el parque. El primer amigo corre alrededor de la pista en 15 minutos, el segundo amigo en 20 minutos y el tercer amigo en 25 minutos. ¿Cuántas vueltas debe dar cada amigo para coincidir en el punto de partida?
El coche de María consumió 30 litros de gasolina en un viaje de 375 km, ¿cuántos litros de gasolina requiere para recorrer 494 km?
¡Prepárate para un desafío intelectual! Inicia el cuestionario.👨🏻🚀🚀🪐
💙Gracias a los anuncios, puedo seguir compartiendo todo lo que te gusta de Math3Logic. ¡Agradezco tu apoyo!
💙Recuerda que puedes encontrar todos los temas aquí Math3logic-Matemáticas. Si no encuentras alguno, ¡pronto lo tendrás disponible ahí mismo!
💙Si algo en la página no funciona o un enlace no se abre, por favor repórtalo por WhatsApp.
💙Recuerden que juntos hacemos un gran equipo 😊🧠💪🏻
Sigue practicando problemas de mínimo común múltiplo
Más temas relacionados
Practicar otros temas
⭐ ¿Te sirvió la información?
Interacción con los anuncios
Quiero disculparme por los anuncios en la página que pueden afectar tu experiencia en Math3logic. Sin embargo, estos anuncios son una forma de apoyarme para que el sitio web pueda seguir creciendo. Si encuentras algún anuncio que te resulte interesante, puedes explorar la información que ofrece
Suscríbete a mi canal de YouTube
Si alguno de los vídeos de la página te resultó útil, sería de gran ayuda que te suscribieras a mi canal de YouTube, dejaras tu comentario o simplemente le dieras ‘me gusta’ al vídeo. Tu apoyo en estas acciones contribuye enormemente al crecimiento del canal y me anima a seguir compartiendo contenido útil
Sígueme e interactúa en mis redes sociales
Tu apoyo es invaluable cuando interactúas con mis publicaciones en redes sociales como Facebook, Instagram, TikTok, YouTube, y más. Agradezco mucho tu participación en estas plataformas.
¿Necesitas apoyo con algún tema de Math3logic?
Si después de ver el material de la página de Math3logic sobre algún tema aún tienes dudas entonces puedes enviarme un mensaje por WhatsApp para apoyarte.








