Perímetro de Figuras
Perímetro
El perímetro de cualquier figura se obtiene sumando las longitudes de todos sus lados.
El perímetro es el contorno o lo que está al rededor de la figura, se mide en unidades lineales (km, m, cm, etc.).
Por ejemplo el perímetro del siguiente cuadrado es:
Perímetro = 7 + 7 + 7 + 7 = 28 cm.

Diferencia entre área y perímetro
El perímetro es lo que está al rededor de la figura.
Para calcular el perímetro se suman todas las longitudes que se encuentran alrededor de la figura no importa que tipo de figura sea. En ciertos casos como en figuras que tienen todos los lados iguales el perímetro puede obtenerse mediante fórmulas que reducen el procedimiento de sumar a una simple multiplicación. Es importante no confundir las fórmulas del perímetro con las fórmulas para calcular el área de una figura.
El área es lo que está dentro de la figura (el relleno). Cada figura tiene su propia fórmula para calcular el área.
Hay una sección completa en donde se aborda el área de figuras geométricas.

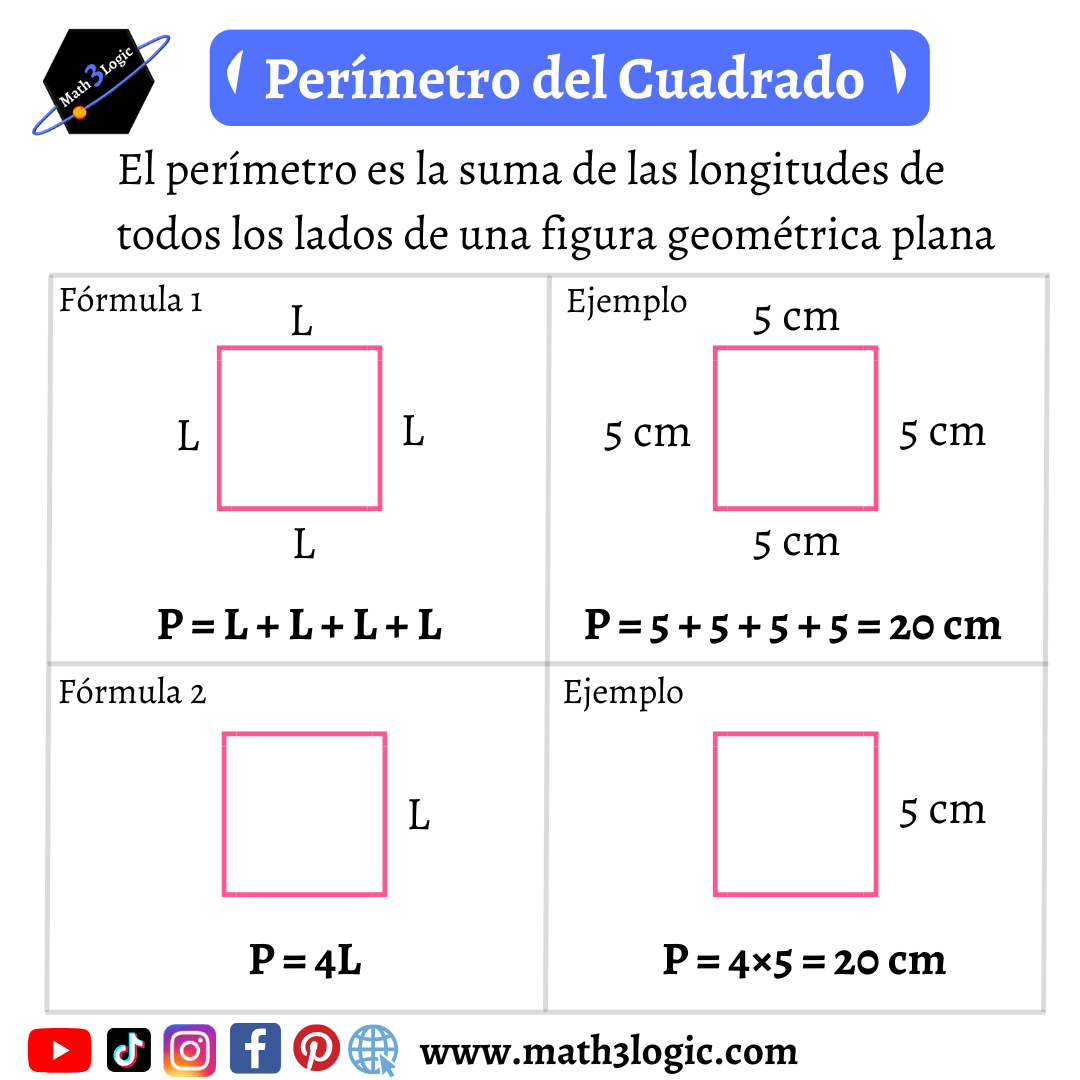
Perímetro del cuadrado
Todos los lados de un cuadrado miden lo mismo. El perímetro del siguiente cuadrado con lado de 9 cm es:
1.- Perímetro = 9 + 9 + 9 + 9 = 36 cm
2.- Perímetro = 4×9 = 36 cm

Perímetro del triángulo
Un triangulo equilátero es el que tiene todos sus lados iguales. El perímetro del siguiente triángulo con lado de 4 cm es:
1.- Perímetro = 4 + 4 + 4 = 12 cm
2.- Perímetro = 3×4 = 12 cm

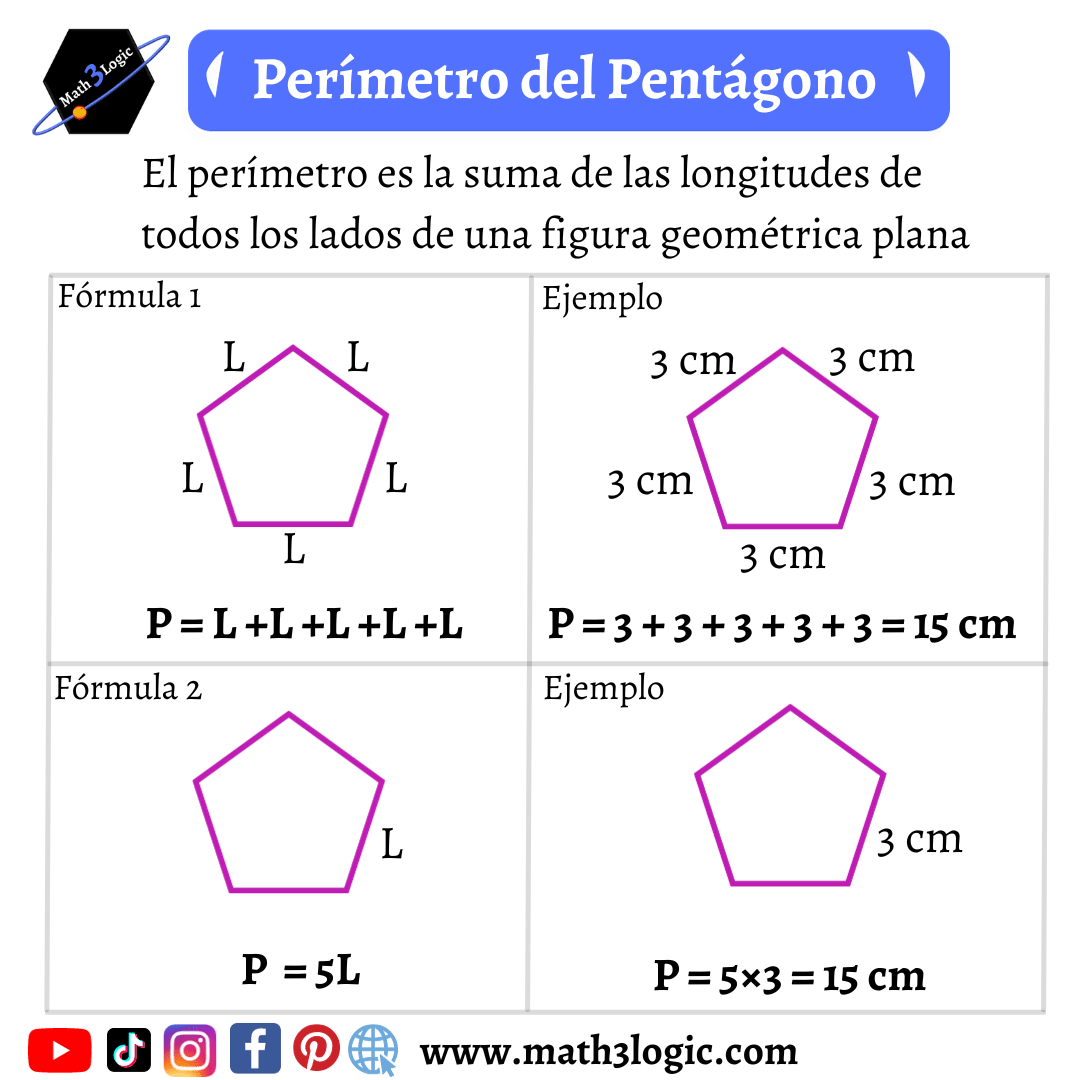
Perímetro de un pentágono
Un pentágono regular es el que tiene todos sus lados iguales. El perímetro del siguiente pentágono con lado de 7 cm es:
1.- Perímetro = 7 + 7 + 7 + 7 + 7 = 35 cm
2.- Perímetro = 5×7 = 35 cm

Perímetro de un rombo
Un rombo tiene todos sus lados iguales. El perímetro del siguiente rombo con lado de 2 cm es:
1.- Perímetro = 2 + 2 + 2 + 2 = 8 cm
2.- Perímetro = 4×2 = 8 cm

Perímetro de un rectángulo
El perímetro del siguiente rectángulo con ancho 3 cm y largo de 14 cm es:
1.- Perímetro = 3 + 14 + 3 + 14 = 34 cm
2.-Perímetro = 2×3 + 2×14 = 6 + 28= 34 cm

Perímetro de un romboide
El perímetro del siguiente romboide con lados de 7 cm, 9 cm, 7 cm y 9 cm es:
1.- Perímetro = 7 + 9 + 7 + 9 = 32 cm
2.- Perímetro = 2×7+ 2×9 = 14 + 18= 32 cm

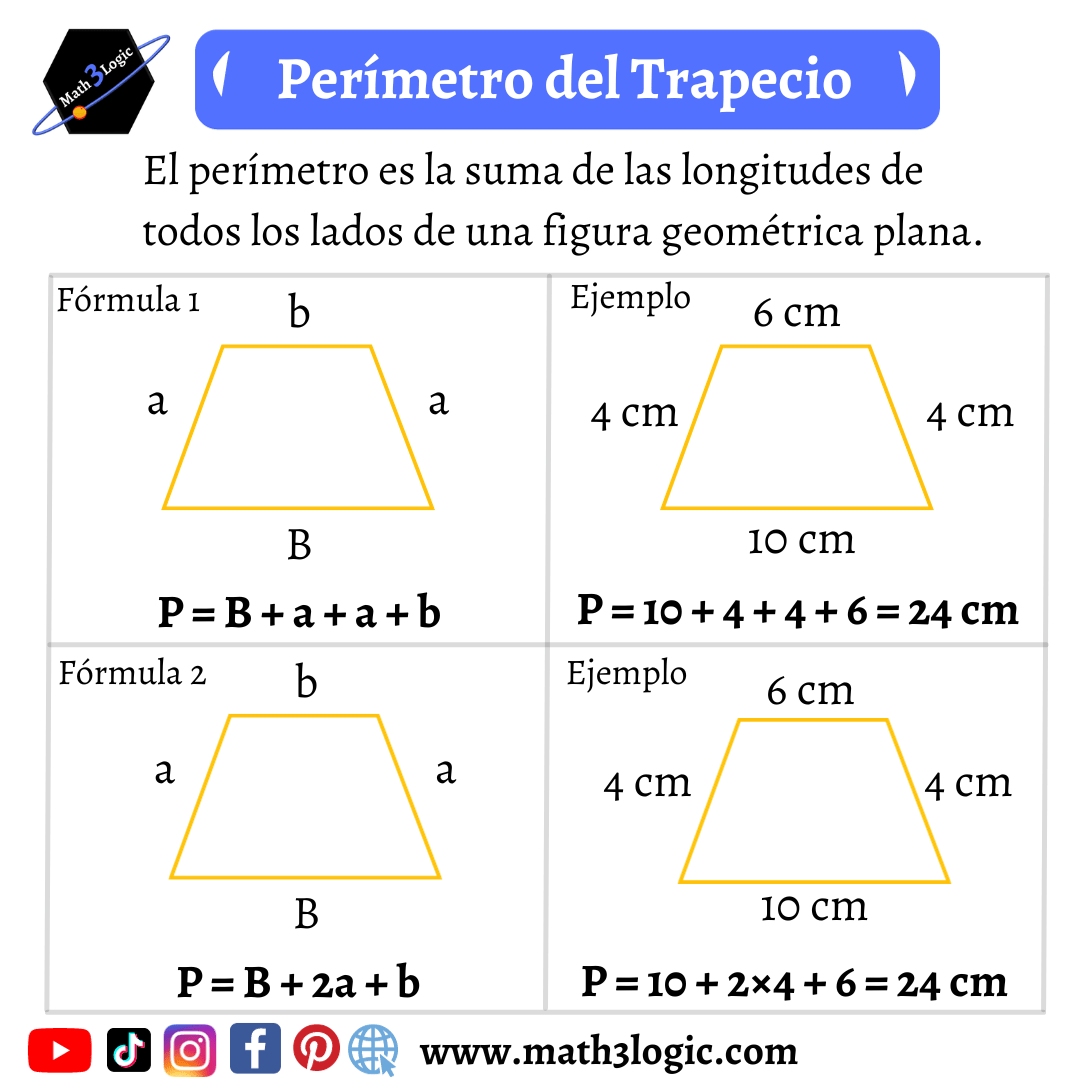
Perímetro de un trapecio
El perímetro del siguiente trapecio con lados de 10 cm, 12 cm, 10 cm y 8 cm es:
1.- Perímetro = 10 + 12 + 10 + 8 = 40 cm
2.- Perímetro = 12 + 8 + 2×10 = 12 + 8 + 20 = 40 cm

Perímetro del triángulo
Un triangulo isósceles es el que tiene todos sus lados distintos. El perímetro del siguiente triángulo con lados de 8 cm, 5 cm y 11 cm es:
1.- Perímetro = 8 + 5 + 11 = 24 cm

Fórmulas para la circunferencia de un círculo
En un círculo, el diámetro (d) es el doble del radio (r), es decir, d = 2r. Por lo tanto, para calcular la circunferencia (el contorno del círculo), se pueden usar dos fórmulas equivalentes:
1.- Circunferencia = 𝝅d
2.- Circunferencia = 2𝝅r

Circunferencia del Círculo
La circunferencia del siguiente círculo con diámetro de 6 cm es:
1.- Circunferencia = 𝝅d = 𝝅×6 = 18.4 cm
2.-Circunferencia = 2𝝅r = 2𝝅(3)= 18.4 cm
Recuerda que el diámetro es el doble del radio d = 2r, en otras palabras, el radio es la mitad del diámetro r = d/2, por lo tanto, si el diámetro es de 6 cm, entonces el radio es de 3 cm. El número Pi se usa como 3.14 para los calculos.

Posibles errores al calcular el perímetro
Cuando calculas el área de una figura en muchas ocasiones se necesita la medida de la altura, sin embargo, no es necesaria para calcular el perímetro cuando la altura no es parte del contorno, la altura regularmente se encuentra dentro o fuera de la figura, observa la imagen.
Error 1 : Sumar la altura de la figura (cuando estas no son parte del contorno) es un error muy común. Por ejemplo en la figura 1 la altura se encuentra dentro del trapecio por lo tanto no es parte del perímetro de la figura así que no se suma esa longitud.
En la figura 2 la altura está fuera de la figura, no es parte del perímetro así que tampoco se suma esa longitud.
Error 2: Observa que en la figura 1 uno de sus lados del trapecio mide 6 cm y el otro lado también mide 6 cm pero no está escrito, por lo que en ocasiones se olvida sumar ese lado por el simple hecho de que no está el valor escrito sin embargo es importante tener cuidado y agregar todas las longitudes que estén en el contorno de la figura.

¿Cómo encontrar el lado que falta de una figura usando su perímetro?
Para resolver problemas de este tipo, existen dos casos:
1.-El primero es cuando conoces el perímetro y todos los lados de la figura son iguales, como en el caso del cuadrado, el rombo y el pentágono regular. En este caso, al encontrar la medida de uno de los lados, automáticamente tendrías la medida de todos los demás, ya que son iguales.
2.-El segundo caso es cuando conoces el perímetro pero no todos los lados de la figura son iguales. En este caso, se te proporciona la medida de los lados, excepto uno de ellos, que es el que quieres encontrar.
Puedes encontrar este tema en la siguiente sección.
Obtener el lado que falta de una figura conociendo su perímetro.
Galería de Imágenes
En Math3logic®️me esfuerzo por crear material divertido y útil para ti🥰. Si decides descargarlo/compartirlo, te pido por favor que dejes el logo intacto y todo lo que representa a Math3logic©️ . También, te agradecería mucho si no modificas las imágenes ni las subes a otros sitios web. ¡Gracias por preferirme y por apoyar el trabajo que hago! 💙
Puedes guardar las imágenes en tus dispositivos 🖥️📱
Ejercicios – Perímetro
Selecciona para ver la fórmula del perímetro de cada figura
¿Cuál es la fórmula para el perímetro?
¿Cuál es la fórmula para el perímetro?
Escoge la respuesta que consideres correcta
El perímetro del cuadrado es:

El perímetro del triángulo es:

El perímetro del pentágono es:

El perímetro del rectángulo es:

El perímetro del rombo es:

La circunferencia del círculo es:

Lee cada problema y selecciona la respueta correcta
Se quiere colocar una valla al rededor de un jardín para evitar que las mascotas se salgan. El jardín tiene forma de cuadrado y uno de sus lados mide 6m ¿cuánto material se necesita para cercar el perímetro del jardín?
Se quiere colocar un listón alrededor de una cancha rectangular con medidas de 65 m de largo y 20 m de ancho ¿cuántos metros de listón se necesitan para poder rodear toda la cancha?
El parque triangular del vecindario está en construcción, se quiere colocar una cinta que diga prohibido el paso, las medidas del parque son 10m, 13m y 25 m ¿cuántos metros se necesitan de cinta para rodear el perímetro del parque?
Si un anillo tiene forma circular y tiene un diámetro de 18 mm, ¿cuál es su circunferencia?
💙Si algo en la página no funciona o un enlace no se abre, por favor repórtalo por WhatsApp.
💙Si descargas/ compartes las imágenes, por favor mantén el logo y todo lo que representa Math3logic©️®️ .
💙Gracias a los anuncios, puedo seguir compartiendo todo lo que te gusta de Math3Logic. ¡Agradezco tu apoyo!
💙Recuerda que puedes encontrar todos los temas aquí Math3logic-Matemáticas. Si no encuentras alguno, ¡pronto lo tendrás disponible ahí mismo!
💙Recuerden que juntos hacemos un gran equipo 😊🧠💪🏻
Comprueba tus conocimientos 🧠
Laboratorio de Juegos 🎮🕹️
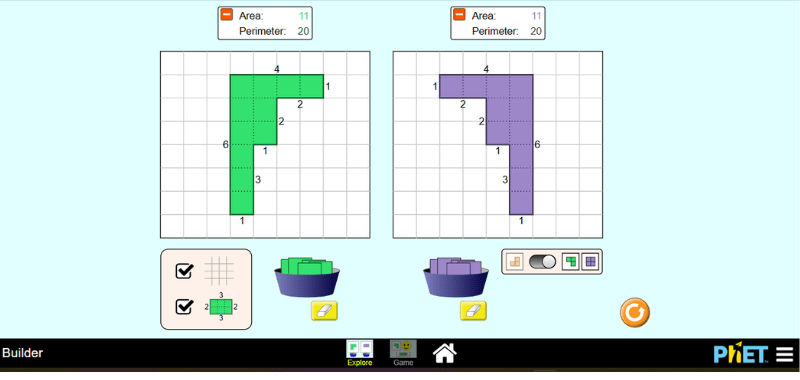
Laboratorio 6🔬
Explora, crea, juega y practica área y perímetro de figuras planas.
¡Prepárate para un desafío intelectual! Inicia el cuestionario.👨🏻🚀🚀🪐
Disfruta los ejercicios y luego regresa a Math3logic para encontrar más actividades y desafíos matemáticos.
¡Aquí siempre habrá más para ti!⭐
Ejercicio 1 - Actividad múltiple 🏅
Ejercicio 2 - Calcula el perímetro🅿️
Ejercicio 3 - ¿Cuál es el perímetro?🤔
Perímetro de rectángulos TQuiz 🐠
Perímetro de triángulos TQuiz 🐠
Perímetro de círculos TQuiz 🐠
Perímetro del trapecio TQuiz 🐠
Perímetro de diferentes figuras TQuiz 🐠
✨Temas relacionados
Practicar otros temas
⭐ ¿Te sirvió la información?
Suscríbete a mi canal de YouTube
Si alguno de los vídeos de la página te resultó útil, sería de gran ayuda que te suscribieras a mi canal de YouTube, dejaras tu comentario o simplemente le dieras ‘me gusta’ al vídeo. Tu apoyo en estas acciones contribuye enormemente al crecimiento del canal y me anima a seguir compartiendo contenido útil
Wishlist de Math3logic - Pequeños Gustos, Gran Inspiración
Tu apoyo significa el mundo para mí. Esta Wishlist de Amazon incluye pequeños detalles y artículos que me inspiran a seguir creando material educativo de calidad para mis estudiantes. ¡Gracias por ser parte de esta aventura matemática!
Interacción con los anuncios
Quiero disculparme por los anuncios en la página que pueden afectar tu experiencia en Math3logic. Sin embargo, estos anuncios son una forma de apoyarme para que el sitio web pueda seguir creciendo. Si encuentras algún anuncio que te resulte interesante, puedes explorar la información que ofrece
Clases particulares en línea
Antes de unirte, ten en cuenta que estas clases no se enfocan en un solo tema aislado. Para llegar al contenido que necesitas, es fundamental comprender las bases primero. ¡Aprender matemáticas es un proceso, y estoy aquí para guiarte en cada paso!
¡Agenda una clase muestra gratis y comienza tu aprendizaje!