Problemas de Máximo Común Divisor
¿Cómo saber cuándo usar el MCD para resolver un problema?
Para saber si un problema se resuelve usando el máximo común divisor (MCD), se debe analizar el contexto y los elementos del problema. El MCD se utiliza regularmente cuando se trata de repartir o distribuir equitativamente recursos.
Reparto de Recursos: Imagina que tienes una cierta cantidad de recursos (como dinero, comida, o tiempo) que deseas repartir equitativamente entre un grupo de personas. El MCD se utiliza para determinar la cantidad máxima que se puede dar a cada persona de manera justa.
También se aplica para distribuir, organizar, simplificar, etc.
Preguntas que te pueden ayudar a determinar si un problema se resuelve usando el MCD
¿El problema te pide el tamaño máximo de un grupo o equipo que pueda ser asignado a una tarea o proyecto? Si necesitas encontrar el tamaño más grande de grupos o equipos idénticos que se pueden formar con un conjunto de objetos, el MCD puede ayudarte a determinar ese tamaño.
¿Estás tratando de simplificar una relación o proporción? Si tienes una relación entre dos cantidades y quieres simplificarla a su forma más reducida, el MCD se usa para simplificar fracciones y expresiones relacionadas.
¿Estás empaquetando objetos en cajas y deseas poner la mayor cantidad de objetos idénticos en cada caja sin desperdiciar espacio? Si necesitas empaquetar objetos en contenedores o cajas y quieres evitar el desperdicio, el mcd se utiliza para encontrar el número máximo de objetos que se pueden empacar sin sobras.
¿El problema te pide dividir algo en partes iguales? Si estás tratando de dividir un recurso (dinero, tiempo, objetos, etc.) en partes iguales, el MCD puede ser relevante para encontrar la cantidad máxima que puedes dividir equitativamente.
Recuerda: Estas preguntas son solo una guía. Lo más importante es analizar con atención el problema y entender sus condiciones para decidir si el MCM es la mejor herramienta.
Problema 1
Una profesora imparte dos cursos: uno con 48 alumnos y otro con 36 alumnos. Quiere distribuir a los alumnos en grupos iguales en cada curso y además, que los grupos sean lo más numerosos posibles. ¿Cuántos grupos tendrá en cada uno de los cursos? ¿Cuántos alumnos tendrá cada grupo en ambos cursos?
Para resolver este problema, primero se encuentra el máximo común divisor de 48 y 36 con el objetivo de saber cuántos alumnos pueden haber en cada grupo para lograr la distribución equitativa.
El máximo común divisor de 48 y 36 es 12 (observa la imagen). Por lo tanto, los alumnos se dividirán en grupos de 12 en ambos cursos.
Para saber cuantos grupos habrá en cada curso se hace los siguiente:
Para el curso con 48 alumnos se tiene
48 ÷ 12 = 4 grupos y cada grupo tendrá 12 alumnos.
Para el curso de 36 alumnos se tiene
36 ÷ 12 = 3 grupos y cada grupo tendrá 12 alumnos.

Problema 2
Jazmín tiene una cuerda de 120 cm de largo y otra de 180 cm de largo. Quiere cortar ambas cuerdas en segmentos de la misma longitud sin desperdiciar nada. ¿Cuál es la longitud máxima que puedes elegir para los segmentos de cuerda?
Para resolver este problema, se necesita encontrar el máximo común divisor de las longitudes de las dos cuerdas (120 cm y 180 cm). El mcd dará la longitud máxima de los segmentos que pueden cortarse de ambas cuerdas sin desperdiciar nada.
El máximo común divisor de 120 y 180 es 60. Por lo tanto, la longitud máxima que puedes elegir para los segmentos de cuerda es de 60 cm.

Problema 3
Se van a fraccionar tres terrenos de 540 m², 720m² y 900m² respectivamente, y se desea que el área de cada lote sea el mayor posible. ¿Cuántos metros cuadrados debe medir cada lote? y ¿Cuántos lotes son en total?
Para maximizar el área de cada lote al fraccionar los terrenos dados, se necesita encontrar el máximo común divisor de las áreas de los terrenos 540 m², 720 m² y 900 m².
El máximo común divisor de 540 m², 720 m² y 900 m² es 180 m²
Por lo tanto, cada lote debe medir . Ahora, para determinar cuántos lotes hay en total, se divide el área total de cada terreno entre el área de cada lote:
Para el primer terreno 540 ÷ 180 = 3 lotes
Para el segundo terreno 720 ÷ 180 = 4 lotes
Para el tercer terreno 900 ÷ 180 = 5 lotes
En total hay 2 + 4 + 5 = 12 lotes.

Problema 4
Tres amigos, Ana, Luis y Elena, tienen 90 manzanas, 120 plátanos y 150 naranjas respectivamente. Quieren dividir las frutas equitativamente entre ellos. ¿Cuál es la mayor cantidad de frutas que pueden tener en cada grupo?
Para resolver el problema, primero se encuentra el máximo común divisor de las cantidades de manzanas, plátanos y naranjas. El mcd dará la mayor cantidad de frutas que pueden tener en cada grupo para que se distribuyan equitativamente.
El mcd de 90, 120 y 150 es 30 (observa la imagen).
Por lo tanto, la mayor cantidad de frutas que pueden tener en cada grupo es de 30 frutas (ya sea manzanas, plátanos o naranjas).

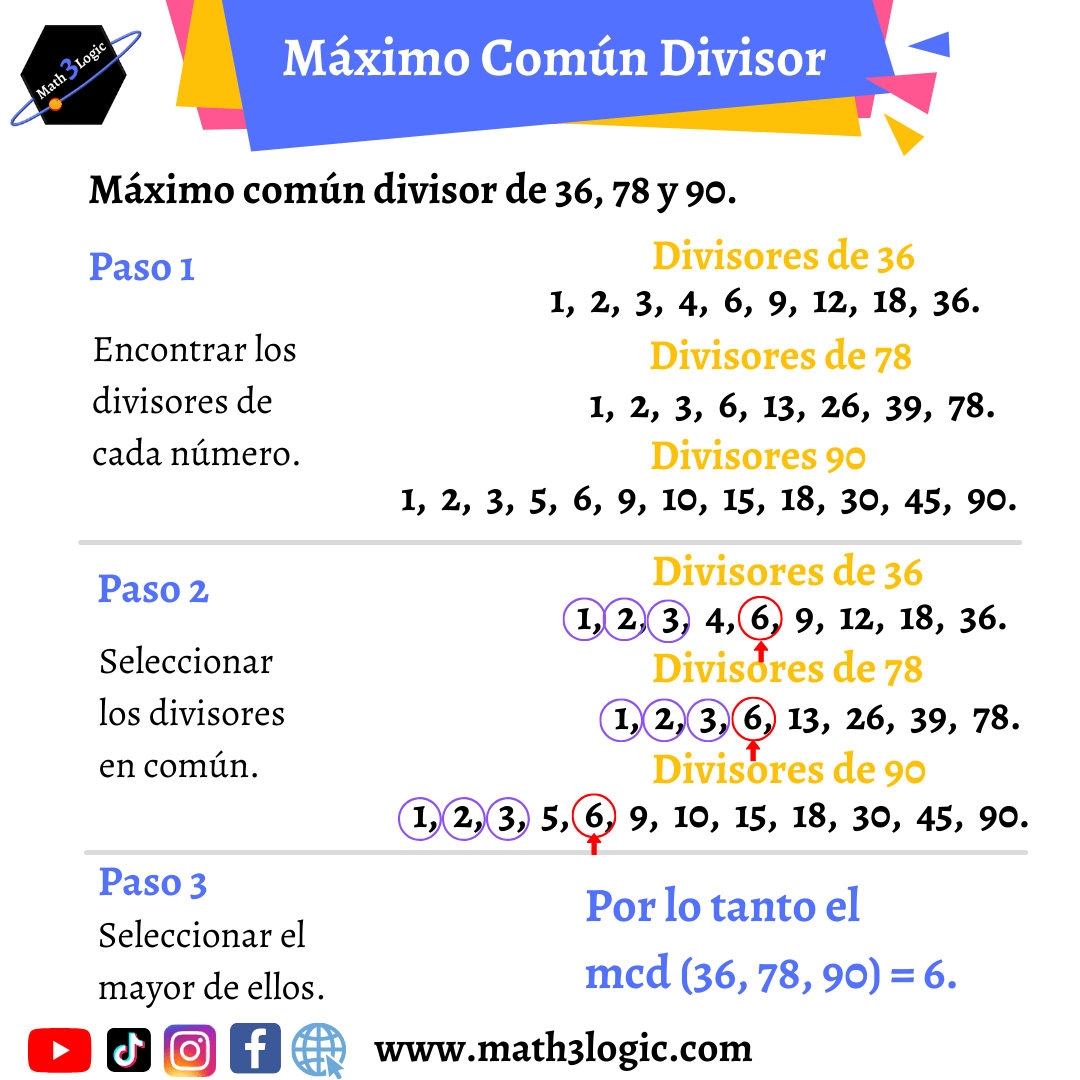
Existen 3 diferentes métodos para encontrar el máximo común divisor
1.- Utilizando los divisores de cada número. Como su nombre lo indica, se identifican los divisores de cada número, se seleccionan los divisores comunes y se elige el mayor de ellos; de ahí el nombre máximo común divisor.
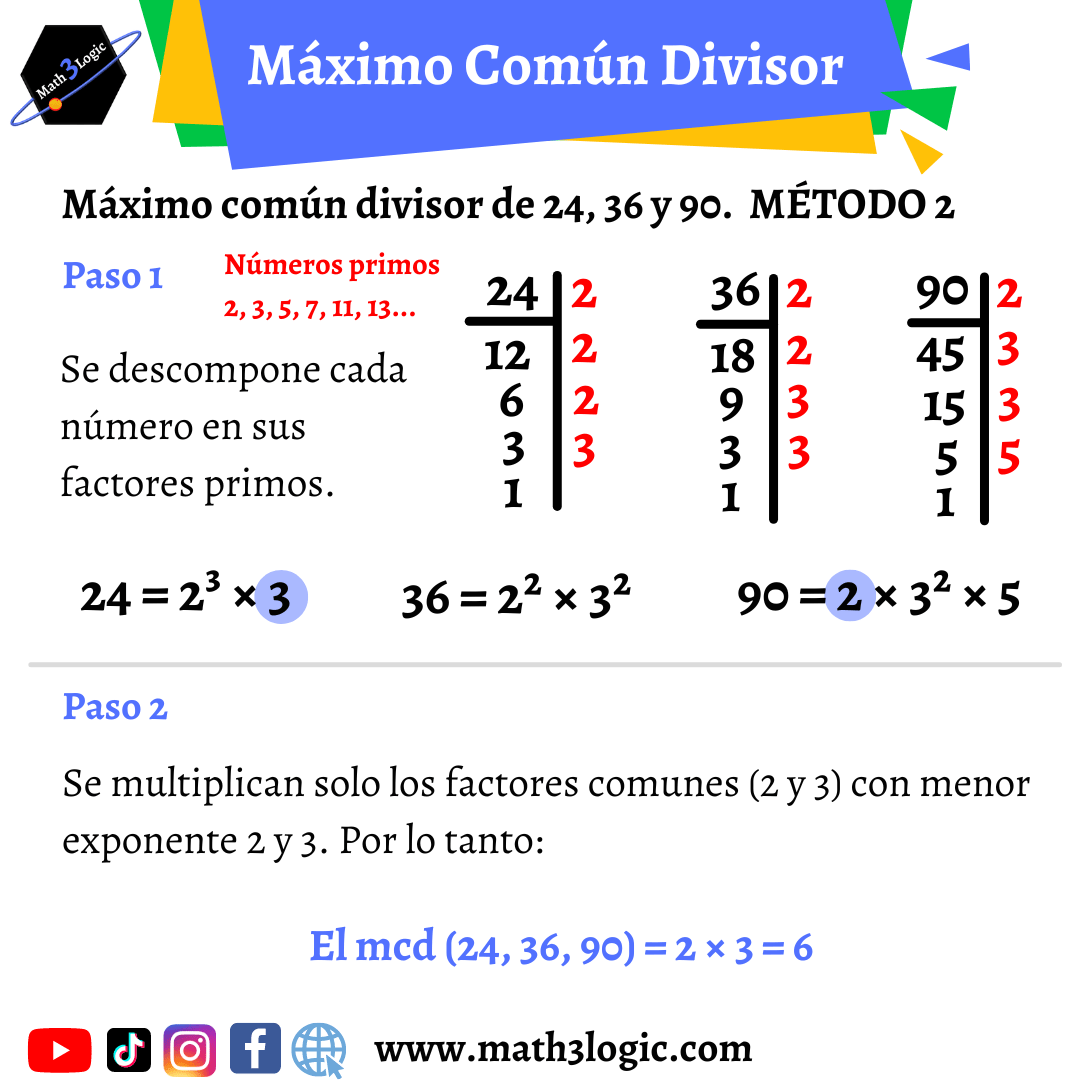
2.- Descomponiendo cada número por separado en factores primos. Se descompone cada número en sus factores primos, luego se toman los factores primos comunes con el menor exponente de cada número. El producto de todos esos factores es el MCD.
3.- Descomponiendo simultáneamente los números. Los números se descomponen en factores primos al mismo tiempo. El producto de estos factores es el MCD.
Cada uno de los procedimientos es explicado paso a paso en la siguiente sección.
Problemas sobre el mínimo común múltiplo (MCM)
¿Cómo saber si tu problema se resuelve mediante el MCM
Para entender si tu problema puede resolverse utilizando el mínimo común múltiplo (MCM), revisa los casos específicos que se explican en el siguiente enlace. Ahí encontrarás una variedad de problemas que se abordan y se resuelven aplicando el concepto del MCM.
Problemas de mínimo común múltiplo (MCM).
Galería de Imágenes
En Math3logic®️me esfuerzo por crear material divertido y útil para ti🥰. Si decides descargarlo/compartirlo, te pido por favor que dejes el logo intacto y todo lo que representa a Math3logic©️ . También, te agradecería mucho si no modificas las imágenes ni las subes a otros sitios web. ¡Gracias por preferirme y por apoyar el trabajo que hago! 💙
Puedes guardar las imágenes en tus dispositivos 🖥️📱
Ejercicios – Problemas de MCD
Lee cada problema y selecciona la respueta correcta
Tienes 60 minutos de matemáticas, 75 minutos de ciencias y 90 minutos de historia para estudiar. Deseas dividir tu tiempo de estudio en bloques iguales para cada materia, sin que quede ningún minuto sin utilizar. ¿Cuál es el máximo número de minutos que puedes estudiar cada materia en un bloque?
Una organización benéfica tiene 150 paquetes de alimentos, 180 paquetes de ropa y 210 paquetes de juguetes para distribuir entre las familias necesitadas. Si desean formar paquetes que contengan la misma cantidad de alimentos, ropa y juguetes, ¿cuál es el máximo número de paquetes de cada tipo que se puede incluir en cada paquete?
Miguel tiene tambos con pintura de 72 litros y de 104 litros para vender la pintura en cubetas con la misma capacidad, se desea la mayor capacidad posible. ¿Cuántos litros contiene cada cubeta? ¿Cuántas cubetas son en total?
Se tienen 96 flores y 120 macetas para decorar un jardín comunitario. Se desea plantar la misma cantidad de flores en cada maceta, no debe sobrar ninguna flor y ni ninguna maceta debe quedar vacía. ¿Cuál es el mayor número de flores que se puede poner en cada maceta y cuántas macetas se necesitarán?
Identifica si el problema se resuelve usando el MCD o no
Quieres hacer pulseras utilizando listones de seda. Tienes 150 cm de listón rosa, 180 cm de listón azul y 210 cm de listón amarillo. Deseas cortar cada listón en segmentos de la misma longitud sin desperdiciar ningún centímetro. ¿Cuál es la longitud máxima de los segmentos que puedes cortar y cuántos segmentos puedes hacer con cada color de listón?
Una escuela organiza un viaje con tres destinos posibles: un zoológico, un museo de ciencias y un parque de diversiones. Si hay 5 autobuses disponibles y cada destino requiere un número diferente de autobuses para acomodar a todos los estudiantes, ¿cuántas combinaciones diferentes de destinos y autobuses pueden elegir para el viaje escolar?
Imagina que tienes 48 caramelos y 60 chocolates que quieres repartir entre tus amigos de manera equitativa. Quieres colocar la misma cantidad de caramelos y chocolates en bolsas para regalar a tus amigos, sin que quede ningún caramelo o chocolate suelto. ¿Cuál es la máxima cantidad de caramelos y chocolates que puedes poner en cada bolsa para que todos los dulces se utilicen y nadie se quede sin recibir?
Laura puede correr 5 kilómetros en 30 minutos. Si quiere saber cuánto tiempo le tomará correr 8 kilómetros a la misma velocidad, ¿cuántos minutos necesitará?
Tú y tus amigos van a un restaurante y deciden pedir pizzas y bebidas. La pizza grande cuesta $20 y las bebidas cuestan $3 cada una. Si pides 3 pizzas y 5 bebidas, ¿cuál será el costo total de la comida?
Imagina que estás organizando una fiesta y tienes 180 empanadas, 240 sándwiches y 300 bollos para distribuir entre los invitados. Deseas repartir estos alimentos equitativamente en bolsas para llevar a casa. ¿Cuál es la mayor cantidad de empanadas, sandwiches y bollos que puedes poner en cada bolsa y cuántas bolsas necesitas?
💙Si algo en la página no funciona o un enlace no se abre, por favor repórtalo por WhatsApp.
💙Si descargas/ compartes las imágenes, por favor mantén el logo y todo lo que representa Math3logic©️®️ .
💙Gracias a los anuncios, puedo seguir compartiendo todo lo que te gusta de Math3Logic. ¡Agradezco tu apoyo!
💙Recuerda que puedes encontrar todos los temas aquí Math3logic-Matemáticas. Si no encuentras alguno, ¡pronto lo tendrás disponible ahí mismo!
💙Recuerden que juntos hacemos un gran equipo 😊🧠💪🏻
¡Prepárate para un desafío intelectual! Inicia el cuestionario.👨🏻🚀🚀🪐
Disfruta los ejercicios y luego regresa a Math3logic para encontrar más actividades y desafíos matemáticos.
¡Aquí siempre habrá más para ti!⭐
Ejercicio 1 - Problemas MCM y MCD 🔎🤔
Ejercicio 2 - Problemas MCM y MCD 2 🔎🤔
Ejercicio 3 - Problemas 2 🕵🏻
✨Temas relacionados
Practicar otros temas
⭐ ¿Te sirvió la información?
Suscríbete a mi canal de YouTube
Si alguno de los vídeos de la página te resultó útil, sería de gran ayuda que te suscribieras a mi canal de YouTube, dejaras tu comentario o simplemente le dieras ‘me gusta’ al vídeo. Tu apoyo en estas acciones contribuye enormemente al crecimiento del canal y me anima a seguir compartiendo contenido útil
Wishlist de Math3logic - Pequeños Gustos, Gran Inspiración
Tu apoyo significa el mundo para mí. Esta Wishlist de Amazon incluye pequeños detalles y artículos que me inspiran a seguir creando material educativo de calidad para mis estudiantes. ¡Gracias por ser parte de esta aventura matemática!
Interacción con los anuncios
Quiero disculparme por los anuncios en la página que pueden afectar tu experiencia en Math3logic. Sin embargo, estos anuncios son una forma de apoyarme para que el sitio web pueda seguir creciendo. Si encuentras algún anuncio que te resulte interesante, puedes explorar la información que ofrece
Clases particulares en línea
Antes de unirte, ten en cuenta que estas clases no se enfocan en un solo tema aislado. Para llegar al contenido que necesitas, es fundamental comprender las bases primero. ¡Aprender matemáticas es un proceso, y estoy aquí para guiarte en cada paso!
¡Agenda una clase muestra gratis y comienza tu aprendizaje!