Jerarquía de Operaciones
¿Qué es la jerarquía de operaciones?
Es el orden correcto en el que se realizan las operaciones. Usualmente, se aplica cuando se combinan varias operaciones en un mismo problema
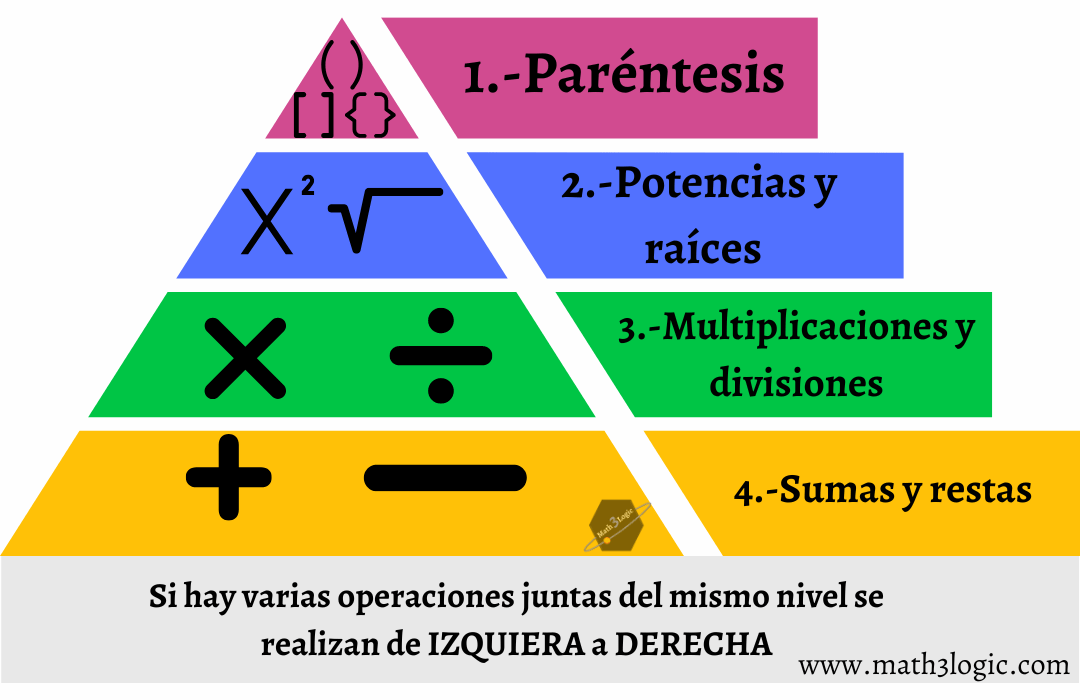
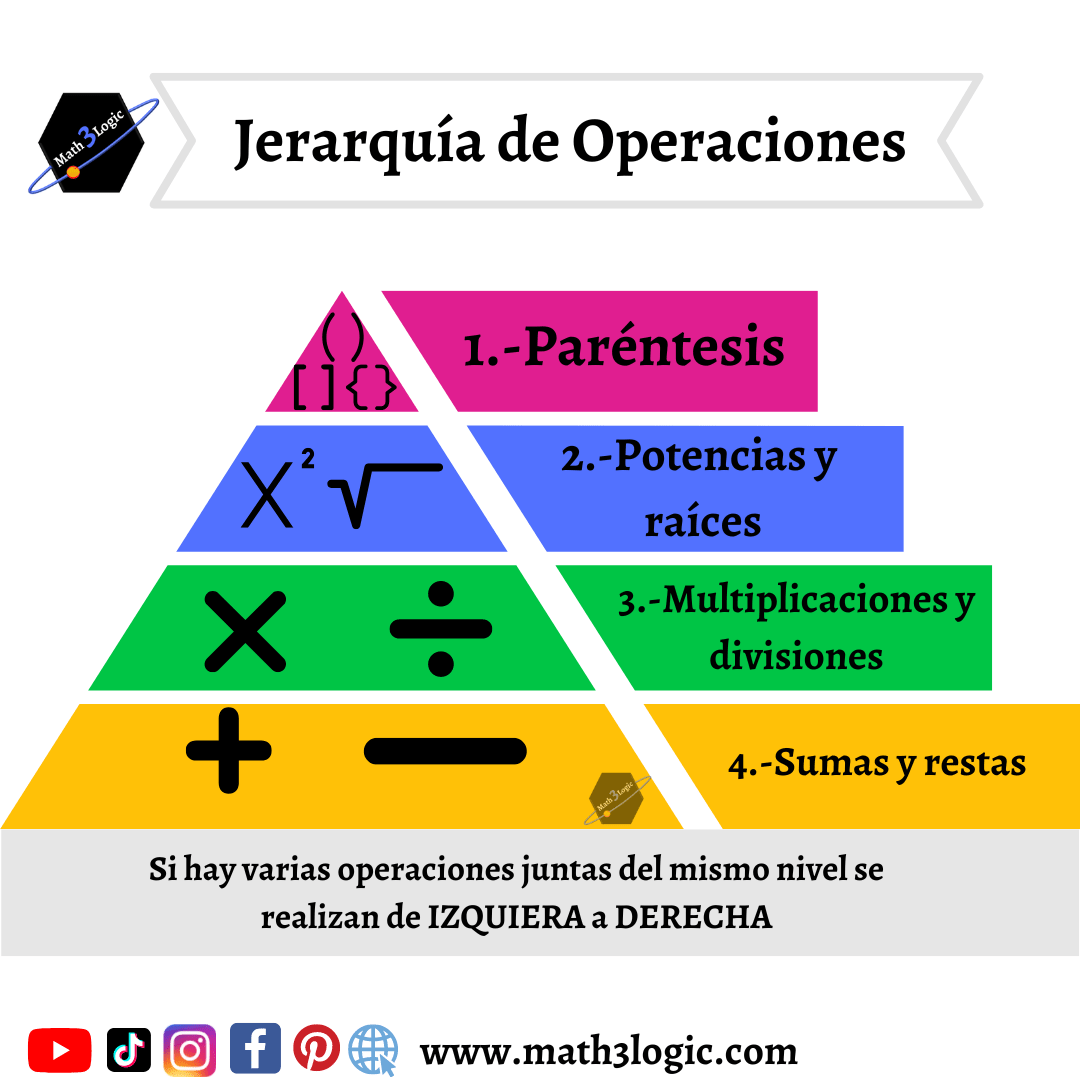
El orden de las operaciones es:
1.- Paréntesis { [ ( ) ] }
2.-Potencias y raíces x²
3.- Multiplicaciones y divisiones ×, ÷
4.- Sumas y restas +, –
Es importante conocer y aplicar correctamente la jerarquía de operaciones para obtener un resultado correcto. Por ejemplo:
5 + 3(4) = 8(4)= 32 Incorrecto, no se respetó la jerarquía
5 + 3(4) = 5 + 12 = 17 Correcto, si se respetó la jerarquía
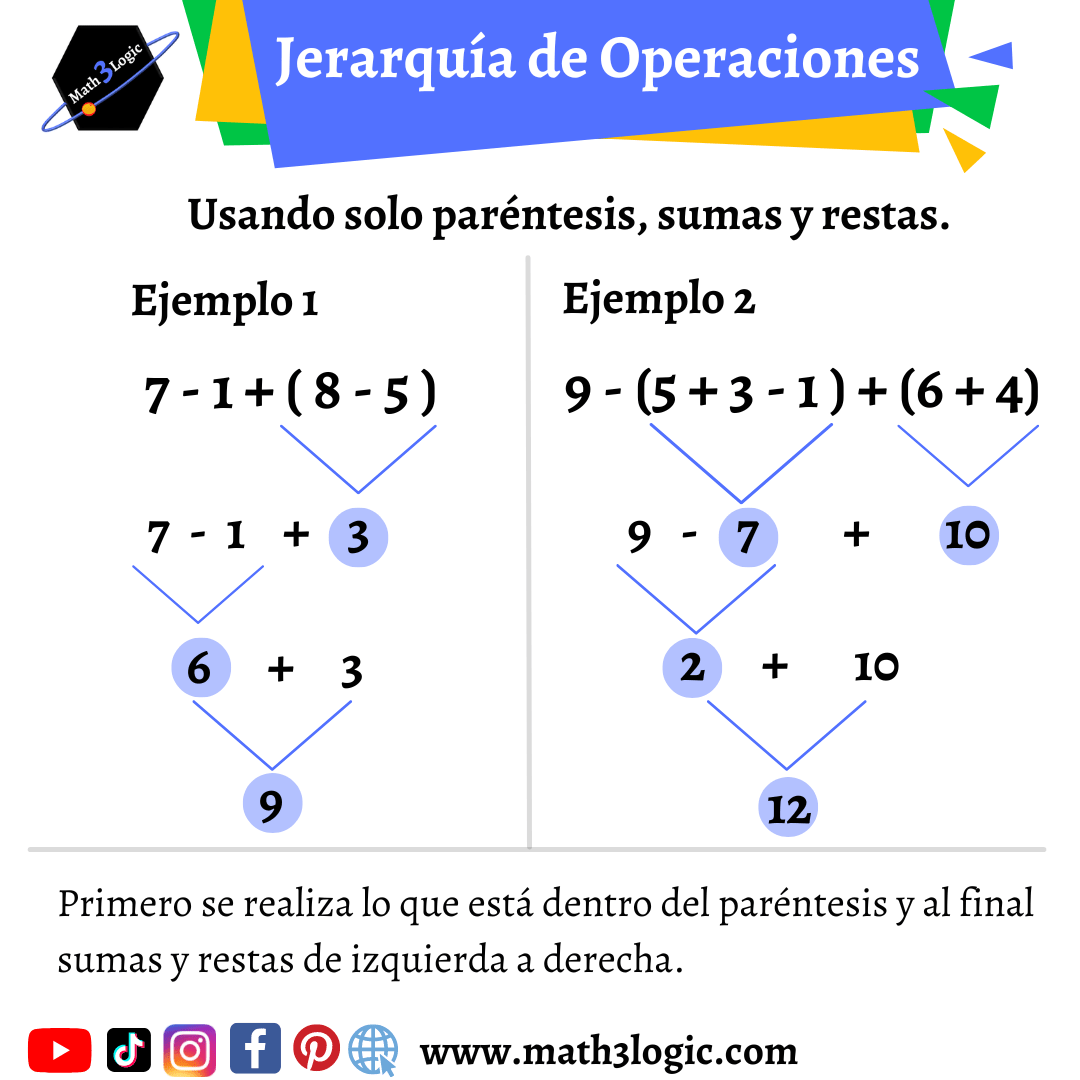
1.- Paréntesis
Primero se realiza cualquier operación dentro del paréntesis, respetando la jerarquía de operaciones si es necesario.
Ejemplos:
- 4 + (12 – 7 ) = 4 + 5 = 9
- (6 + 1 ) – 3 = 7 – 3 = 4
- 15 – (8 – 6) = 15 – 2 = 13
Es importante recordar que las multiplicaciones también pueden representarse con paréntesis, por lo que deben realizarse cuando corresponda según la jerarquía de operaciones.
Ejemplos:
- 3(5 – 1 ) = 3(4) = 12
- 7(2 + 3 ) – 9 = 7(5) – 9 = 35 – 9 = 26
- 4(12÷2) = 4(6) = 24
Recuerda que dentro de los paréntesis también se debe respetar la jerarquía de operaciones.
Ejemplos:
- 1 + ( 10 – 2(3) ) = 1 + (10 – 6) = 1 + 4 = 5
- 7 + (16 ÷ 2 – 5) = 7 + (8 – 5 ) = 7 + 3 = 10
2.-Potencias y raíces
En segundo lugar, están las potencias y las raíces. Ambas tienen el mismo nivel de prioridad, así que se pueden realizar en cualquier orden. Sin embargo, si aparecen juntas en una misma expresión, se resuelven de izquierda a derecha.
Ejemplos:
- √4 + 3² = 2 + 9 = 11
- √16 ÷ 2 = 4 ÷ 2 = 2
- 5² – √9( 4) = 25 – 3(4) = 25 – 12 = 13
- 4( 2³ + 1) = 4(8 + 1) = 4( 9 ) = 36
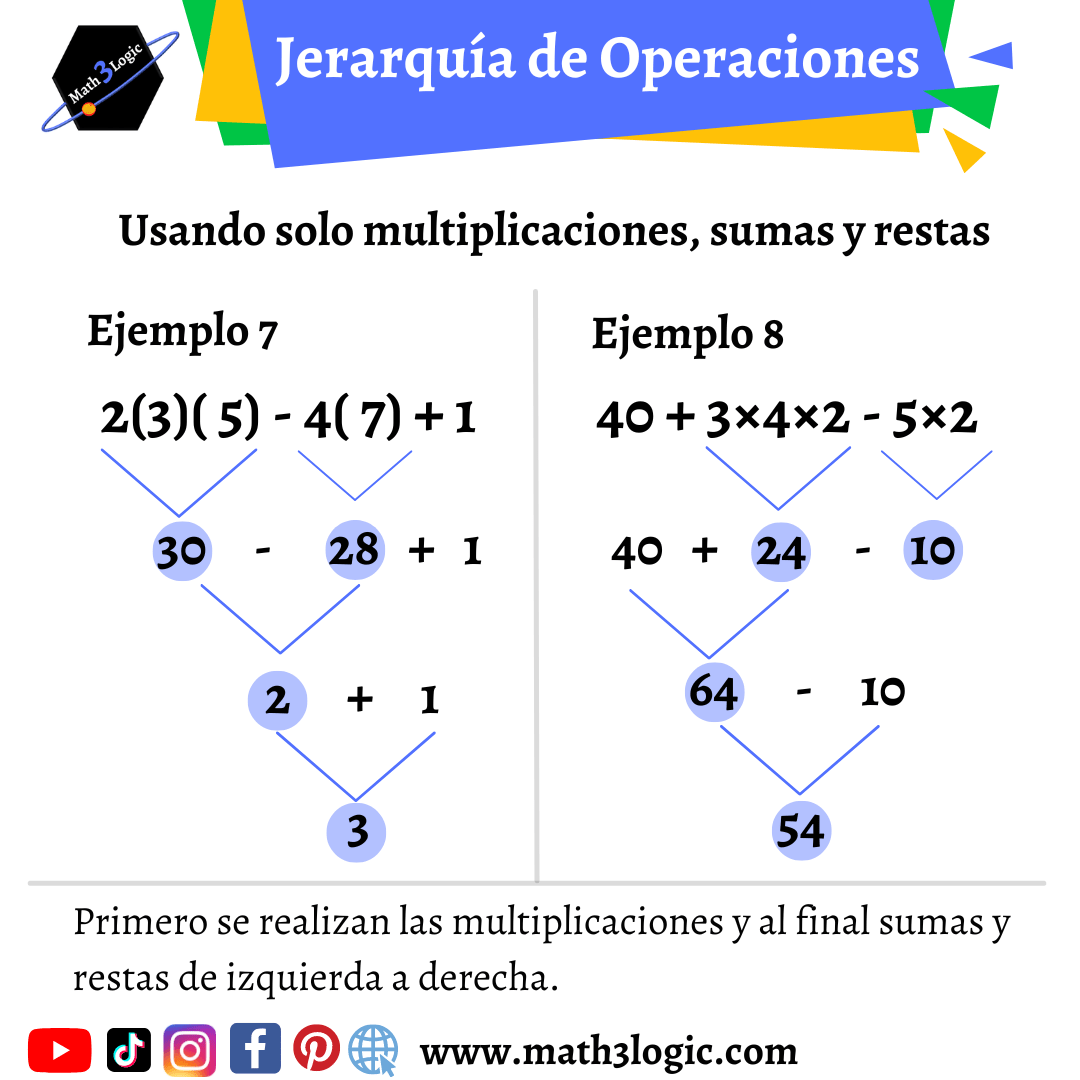
3.-Multiplicaciones y divisiones
En tercer lugar, están las multiplicaciones y divisiones. Ambas tienen el mismo nivel de prioridad, por lo que cualquiera puede realizarse primero. Sin embargo, si aparecen juntas en una expresión, se resuelven de izquierda a derecha.
Ejemplos:
- (4 × 3) ÷ 2 = 12 ÷ 2 = 6
- 20 ÷ 5 + 3 × 6 = 4 + 18 = 22
- 6(3) – 2( 7 ÷ 7 ) = 18 – 2(1) = 18 – 2 = 16
4.- Sumas y restas
En cuarto lugar, están las sumas y restas. Estas también tienen el mismo nivel de prioridad. Sin embargo, al ser la última operación, suelen aparecer juntas en la expresión, por lo que deben resolverse de izquierda a derecha.
Ejemplos:
- 12 – 2 + 5 – 6 = 10 + 5 – 6 = 15 – 6 = 9
- 3(5) + 2² – 4 ÷ 4 = 15 + 4 – 1 = 18
Toma en cuenta que, a pesar de ser la última operación, si dentro de un paréntesis hay sumas y restas, estas se realizarán primero.
16 – 2(8 – 1 + 3 – 4 ) = 16 – 2(6) = 16 – 12 = 4
Signos de agrupación
( ), [ ] y { }
Orden de signos de agrupación ( ), [ ] y { }
Los signos de agrupación se utilizan para establecer un orden en las operaciones; generalmente se emplean en operaciones muy largas. El orden en el que se realizan es el siguiente:
1.- Paréntesis ( )
2.- Corchetes [ ]
3.- Llaves { }
Esto indica que primero se realizan las operaciones dentro de los paréntesis, luego las que están dentro de los corchetes y, al final, las que se encuentran dentro de las llaves. Por lo general, se resuelven de adentro hacia afuera.
Ejemplos:
- ( 8 – 5 ) = 3
- [(13 – 7 ) + 8 ÷ 2] = [6 + 4] = 10
- [ 15 – 2 ( 9 – 3) ] = [15 – 2(6)] = [15 – 12] = 3
- { 9 + [2(7 – 4) ] } = {9 + [2(3)]} ={9+6}=15
Recuerda que, cuando hay un número fuera de los signos de agrupación, significa que debes multiplicar ese número por el resultado obtenido dentro de los signos de agrupación.
Ejemplos:
2( 5 – 1 ) = 2(4) = 8
4[ 7 + 3 ] = 4[10] = 40
6{ 2 + 11} = 6{ 13 } = 78
Cuando te acostumbres y tengas práctica, podrás realizar varias operaciones al mismo tiempo, aunque sean de diferentes niveles en la jerarquía, siempre siguiendo un orden, con el objetivo de ahorrar algunos pasos.
Galería de Imágenes
En Math3logic®️me esfuerzo por crear material divertido y útil para ti🥰. Si decides descargarlo/compartirlo, te pido por favor que dejes el logo intacto y todo lo que representa a Math3logic©️ . También, te agradecería mucho si no modificas las imágenes ni las subes a otros sitios web. ¡Gracias por preferirme y por apoyar el trabajo que hago! 💙
Puedes guardar las imágenes en tus dispositivos 🖥️📱
Ejemplos- Jerarquía de Operaciones
| Nivel 1 - Paréntesis |
|---|
| 2 + (8 - 3)
2 + 5 7 |
| (10 - 6) + 5
4 + 5 9 |
| 20 - (15 - 2) + (9 + 3)
20 - 13 + 12 7 + 12 19 |
| (12 - 5) - (4 - 1) + (7 + 3)
7 - 3 + 10 4 + 10 14 |
| Nivel 2 - Potencias y raíces |
|---|
| 9 - 2²
9 - 4 5 |
| √25 + 7
5 + 7 12 |
|
40 - 3² + √16 + 3
40 - 9 + 4 + 3 31 + 4 + 3 38 |
| 9² - √49 + 2³ + √36 - 1
81 - 7 + 8 + 6 - 1 74 + 8 + 6 - 1 87 |
| Nivel 3 - Multiplicación y división |
|---|
| 11 + 7(4)
11 + 28 39 |
| 75 ÷ 15 - 3
5 - 3 2 |
| 58 - 3·6 + 21÷3 - 9
58 - 18 + 7 - 9 40 + 7 - 9 38 |
| 5( 18 ÷ 2) + 3·8 - 10( 8 ÷ 2 )
5(9) + 24 - 10(4) 45 + 24 - 40 29 |
| Combinando operaciones |
|---|
| 100 - 2(5 + 4) - 4² + 25÷5 - √9
100 - 2(9) - 16 + 5 - 3 100 - 18 - 16 + 5 - 3 68 |
| 7(9 - 3 + 2²) - 5·4 + √4(35÷7)
7 (9 - 3 + 4) - 20 + 2(35÷7) 7(10) - 20 + 2(5) 70 - 20 + 10 60 |
|
25 + 3(6÷2) + √64 - (12 - 5) - 2³
25 + 3(3) + 8 - 7 - 8 25 + 9 + 8 - 7 - 8 27 |
Signos de agrupación
( ), [ ] y { }
| Paréntesis y corchetes |
|---|
| [30 - 2(5 + 4) - 1³]
[30 - 2(9) - 1] [30 - 18 - 1] 11 |
| 85 -[3(10 - 2²) + √36÷2]
85 - [3(10 - 4) + 6÷2] 85 - [3(6) + 3] 85 - [18 + 3] 85 - 21 64 |
| 4(6÷2) + 5[2(10 - 7) + 9]
4(3) + 5[2(3) + 9] 12 + 5[6 + 9] 12 + 5[15] 12 + 75 87 |
| Paréntesis, corchetes y llaves |
|---|
| 1 + {27 - 2[(8 - 3) + √49]}
1 + {27 - 2[5 + 7]} 1 + {27 - 2[12]} 1 + {27 - 24} 1 + 3 4 |
| 8² - 3{5 + 4[6 - (20÷4)] - 1}
8² - 3{5 + 4[6 - 5] - 1} 8² - 3{5 + 4[1] - 1} 8² - 3{5 + 4 - 1} 8² - 3{8} 64 - 24 40 |
|
{55 + [90÷9 - 1] - 6[(8-5) + 4]} + 10
{55 + [10 - 1] -6[3 + 4]} + 10 {55 + 9 - 6[7]} + 10 {55 + 9 - 42} + 10 {64-42} + 10 22 + 10 32 |
Ejercicios – Jerarquía de Operaciones
Resuelve y ve si tu respuesta es correcta
Resuelve:
Resuelve:
Resuelve:
Resuelve:
Resuelve:
Resuelve:
Escoge la respuesta que consideres correcta
¿Cuál es el resultado?
¿Cuál es el resultado?
¿Cuál es el resultado?
¿Cuál es el resultado?
¿Cuál es el orden correcto con el que se deben de realizar las operaciones? (Jerarquía de operaciones)
¿Cuál es el orden de los signos de agrupación?
¿Cuál es el resultado?
¿Cuál es el resultado?
Resuelve las operaciones y luego selecciona para ver la respuesta
Aplica la jerarquía de operaciones
Aplica el orden de los signos de agrupación y la jerarquía de operaciones
Selecciona la respuesta correcta aplicando la jerarquía de operaciones
¿Cuál es el resultado final?

¿Cuál es el resultado final?
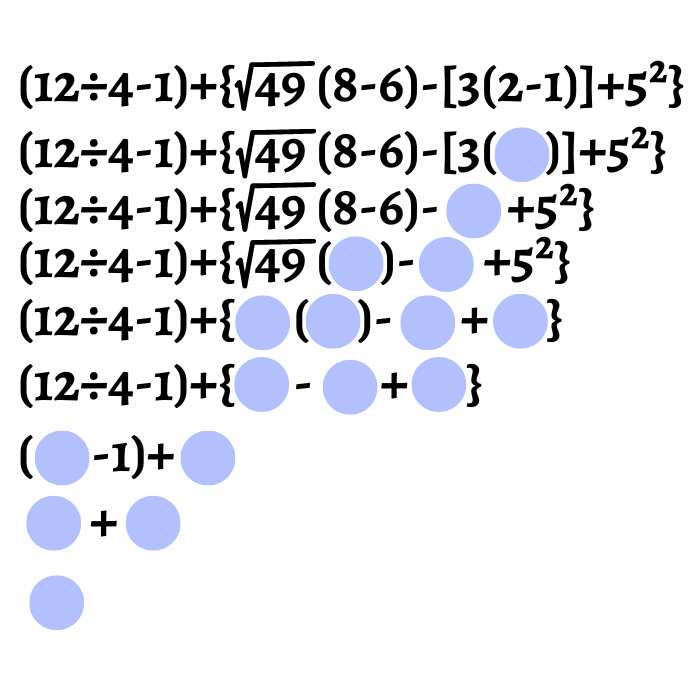
¿Cuál es el resultado final?
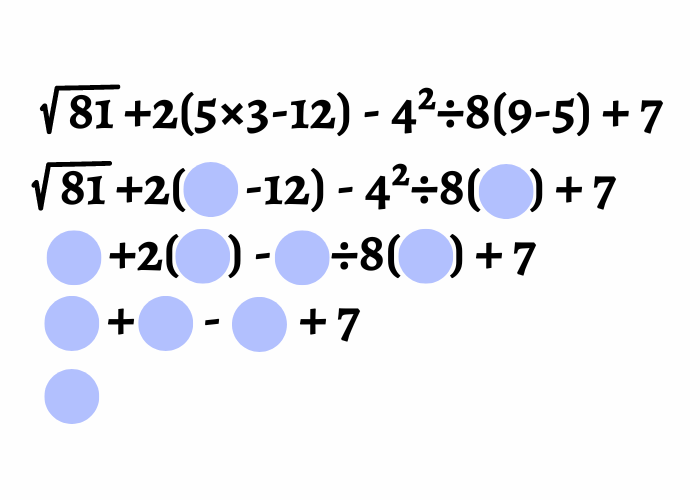
💙Si algo en la página no funciona o un enlace no se abre, por favor repórtalo por WhatsApp.
💙Si descargas/ compartes las imágenes, por favor mantén el logo y todo lo que representa Math3logic©️®️ .
💙Gracias a los anuncios, puedo seguir compartiendo todo lo que te gusta de Math3Logic. ¡Agradezco tu apoyo!
💙Recuerda que puedes encontrar todos los temas aquí Math3logic-Matemáticas. Si no encuentras alguno, ¡pronto lo tendrás disponible ahí mismo!
💙Recuerden que juntos hacemos un gran equipo 😊🧠💪🏻
Comprueba tus conocimientos🧠
Laboratorio de Juegos 🎮🕹️
¡Prepárate para un desafío intelectual! Inicia el cuestionario.👨🏻🚀🚀🪐
Disfruta los ejercicios y luego regresa a Math3logic para encontrar más actividades y desafíos matemáticos.
¡Aquí siempre habrá más para ti!⭐
Ejercicio 1 - TQuiz 🐠
Ejercicio 2 - Selecciona 🔢🤖
Ejercicio 3 - Jerarquía de operaciones 😊
Ejercicio 4 - TQuiz Nivel 2🐠
Ejercicio 5 - Orden de las operaciones 🆗
⭐ ¿Te sirvió la información?
Practicar otros temas
⭐ ¿Te sirvió la información?
Suscríbete a mi canal de YouTube
Si alguno de los vídeos de la página te resultó útil, sería de gran ayuda que te suscribieras a mi canal de YouTube, dejaras tu comentario o simplemente le dieras ‘me gusta’ al vídeo. Tu apoyo en estas acciones contribuye enormemente al crecimiento del canal y me anima a seguir compartiendo contenido útil
Wishlist de Math3logic - Pequeños Gustos, Gran Inspiración
Tu apoyo significa el mundo para mí. Esta Wishlist de Amazon incluye pequeños detalles y artículos que me inspiran a seguir creando material educativo de calidad para mis estudiantes. ¡Gracias por ser parte de esta aventura matemática!
Interacción con los anuncios
Quiero disculparme por los anuncios en la página que pueden afectar tu experiencia en Math3logic. Sin embargo, estos anuncios son una forma de apoyarme para que el sitio web pueda seguir creciendo. Si encuentras algún anuncio que te resulte interesante, puedes explorar la información que ofrece
Clases particulares en línea
Antes de unirte, ten en cuenta que estas clases no se enfocan en un solo tema aislado. Para llegar al contenido que necesitas, es fundamental comprender las bases primero. ¡Aprender matemáticas es un proceso, y estoy aquí para guiarte en cada paso!
¡Agenda una clase muestra gratis y comienza tu aprendizaje!